
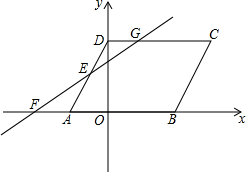
 在平面直角坐标系中,O是坐标原点,平行四边形ABCD的顶点A的坐标为(-2,0),点D的坐标为(0,2$\sqrt{3}$),且AB:AD=3:2,点B在x轴的正半轴上,点E为线段AD的中点,过点E的直线与x轴交于点F(-4,0),与DC交于点G.
在平面直角坐标系中,O是坐标原点,平行四边形ABCD的顶点A的坐标为(-2,0),点D的坐标为(0,2$\sqrt{3}$),且AB:AD=3:2,点B在x轴的正半轴上,点E为线段AD的中点,过点E的直线与x轴交于点F(-4,0),与DC交于点G.分析 (1)要求?ABCD的面积,只要求出AB的长和OD的长即可,由点A(-2,0),点D(0,2$\sqrt{3}$),∠AOD=90°,可以得到OD的长和AD的长,由AB:AD=3:2,可以得到AB的长,本题得以解决;
(2)要求点G的坐标,由题意可得点E为线段AD的中点,通过证明△DEG与△AEF全等,可以说明点E为线段FG的中点,从而可以得到点G的坐标;
(3)要求直线l的解析式,由过点F的直线l平分?ABCD的面积,可以得到直线l过平行四边形的中心,由题意可以得到平行四边形的中心的坐标,从而可以求出直线l的解析式.
解答 解:(1)∵点A(-2,0),点D(0,2$\sqrt{3}$),∠AOD=90°,
∴OA=2,OD=$2\sqrt{3}$,
∴AD=$\sqrt{O{A}^{2}+O{D}^{2}}=\sqrt{{2}^{2}+(2\sqrt{3})^{2}}=4$,
∵AB:AD=3:2,
∴AB=6,
∴S?ABCD=AB•OD=6×$2\sqrt{3}$=12$\sqrt{3}$;
(2)∵点E是线段AD的中点,
∴点E(-1,$\sqrt{3}$),
设点G的坐标为(x,y),
∵DG∥AB,
∴∠DGE=∠AFE,
在△DGE和△AFE中,
$\left\{\begin{array}{l}{∠DGE=∠AFE}\\{∠AEF=∠DEG}\\{ED=EA}\end{array}\right.$,
∴△DGE≌△AFE(AAS),
∴FE=EG,
即点E为线段FG的中点,
∵点F(-4,0),点G(x,y),点E(-1,$\sqrt{3}$),
∴$\frac{-4+x}{2}$=-1,$\frac{0+y}{2}$=$\sqrt{3}$,
解得,x=2,y=2$\sqrt{3}$,
即点G的坐标是(2,2$\sqrt{3}$);
(3)∵过点F的直线l平分?ABCD的面积,
∴直线l过平行四边形的中心点H,如右图所示,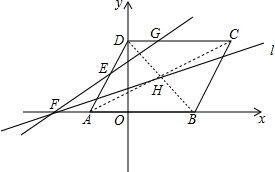
∵点D(0,2$\sqrt{3}$),点B(4,0),
∴点H(2,$\sqrt{3}$),
设过点F(-4,0),点H(2,$\sqrt{3}$)的直线l的解析式为y=kx+b,
$\left\{\begin{array}{l}{-4k+b=0}\\{2k+b=\sqrt{3}}\end{array}\right.$,
解得,$\left\{\begin{array}{l}{k=\frac{\sqrt{3}}{6}}\\{b=\frac{2\sqrt{3}}{3}}\end{array}\right.$
即直线l的解析式为y=$\frac{\sqrt{3}}{6}x+\frac{2\sqrt{3}}{3}$.
点评 本题考查平行四边形综合题,解题的关键是明确题意,找出所求问题需要的条件,找出题目中的隐含条件,尤其是第(3)问中过点F的直线l平分?ABCD的面积,可知直线l过平行四边形的中心,利用数形结合的思想解答.


科目:初中数学 来源: 题型:填空题
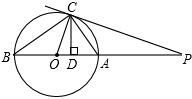 如图,点P是⊙O的直径BA延长线上一点,PC与⊙O相切于点C,CD⊥AB,垂足为D,连接AC,BC,OC,那么下列结论:①PC2=PA•PB;②PC•OC=OP•CD;③OA2=OD•OP;④CD2>BD•AD,正确的有①②③.
如图,点P是⊙O的直径BA延长线上一点,PC与⊙O相切于点C,CD⊥AB,垂足为D,连接AC,BC,OC,那么下列结论:①PC2=PA•PB;②PC•OC=OP•CD;③OA2=OD•OP;④CD2>BD•AD,正确的有①②③.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
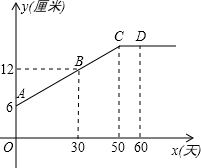 某生物小组观察一植物生长,得到植物高度y(单位:cm)与观察时间x(单位:天)的关系,并画出如图所示的图象(CD∥x轴)
某生物小组观察一植物生长,得到植物高度y(单位:cm)与观察时间x(单位:天)的关系,并画出如图所示的图象(CD∥x轴)查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com