
科目:初中数学 来源: 题型:填空题
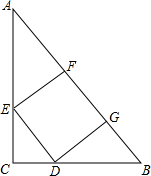 如图所示,Rt△ABC中,AC=4,BC=3,正方形DEFG的顶点分别在Rt△ABC的边上,则正方形的边长为$\frac{60}{37}$.
如图所示,Rt△ABC中,AC=4,BC=3,正方形DEFG的顶点分别在Rt△ABC的边上,则正方形的边长为$\frac{60}{37}$.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
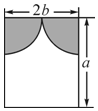 长方形窗户上的装饰物如图所示,它是由半径均为b的两个四分之一圆组成,则能射进阳光部分的面积是( )
长方形窗户上的装饰物如图所示,它是由半径均为b的两个四分之一圆组成,则能射进阳光部分的面积是( )| A. | 2a2-πb2 | B. | 2a2-$\frac{π}{2}$b2 | C. | 2ab-πb2 | D. | 2ab-$\frac{π}{2}$b2 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 已知a,b,c在数轴上的位置如图所示,所对应的点分别为A,B,C.
已知a,b,c在数轴上的位置如图所示,所对应的点分别为A,B,C.查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 ”表示数据输入、输出框;用“
”表示数据输入、输出框;用“ ”表示数据处理和运算框;用“
”表示数据处理和运算框;用“ ”表示数据判断框(根据条件决定执行两条路径中的某一条)
”表示数据判断框(根据条件决定执行两条路径中的某一条) ”内,应填×5;第二个运算框“
”内,应填×5;第二个运算框“ ”内,应填-3;
”内,应填-3;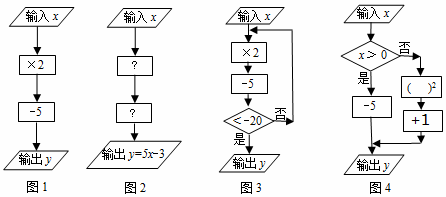
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com