
 ��ͼ��ʾ��ij��ѧ�С��ѡ������С�Ӷ�����BC�ĸ߶ȣ�������б����D����ô�������B��������30�㣬����������������6�����µ�A������A����ô�������B��������48�㣬��б��AF���¶�i=1��$\sqrt{3}$��������ĸ߶�Ϊ������������������������ο����ݣ�sin48���0.74��cos48���0.67��tan48���1.11��$\sqrt{3}$��1.732��
��ͼ��ʾ��ij��ѧ�С��ѡ������С�Ӷ�����BC�ĸ߶ȣ�������б����D����ô�������B��������30�㣬����������������6�����µ�A������A����ô�������B��������48�㣬��б��AF���¶�i=1��$\sqrt{3}$��������ĸ߶�Ϊ������������������������ο����ݣ�sin48���0.74��cos48���0.67��tan48���1.11��$\sqrt{3}$��1.732��| A�� | 11�� | B�� | 12�� | C�� | 13�� | D�� | 14�� |
���� ���ȹ���D��DM��BC�ڵ�M��DN��AC�ڵ�N����FA���±�i=1��$\sqrt{3}$��DA=6�������AN��DN�ij���Ȼ��������ĸ߶�Ϊx��������б����A����ô�������B��������48�㣬�ɵ�AC=$\frac{x}{1.11}$�������ڡ�ADM�У�$\frac{AM}{DM}$=$\frac{\sqrt{3}}{3}$���ɵ�x-3=��3$\sqrt{3}$+$\frac{x}{1.11}$��•$\frac{\sqrt{3}}{3}$���̶���ô𰸣�
��� 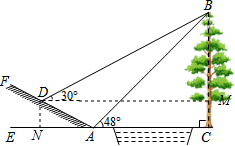 �⣺����D��DM��BC�ڵ�M��DN��AC�ڵ�N��
�⣺����D��DM��BC�ڵ�M��DN��AC�ڵ�N��
���ı���DMCN�Ǿ��Σ�
��DA=6��б��FA���±�i=1��$\sqrt{3}$��
��DN=$\frac{1}{2}$AD=3��AN=AD•cos30��=6��$\frac{\sqrt{3}}{2}$=3$\sqrt{3}$��
������ĸ߶�Ϊx��
����б����A����ô�������B��������48�㣬
��tan48��=$\frac{BC}{AC}$��1.11��
��AC=$\frac{x}{1.11}$��
��DM=CN=AN+AC=3$\sqrt{3}$+$\frac{x}{1.11}$��
���ڡ�ADM�У�$\frac{AM}{DM}$=$\frac{\sqrt{3}}{3}$��
��x-3=��3$\sqrt{3}$+$\frac{x}{1.11}$��•$\frac{\sqrt{3}}{3}$��
��ã�x��13��
������BCԼ13�ף�
��ѡ��C��
���� ���⿼����ǽ�ֱ�������ε�Ӧ��-���Ǹ������⣬�ܽ������ǹ���ֱ�������Σ������ͼ���������Ǻ�����ֱ���������ǽ���Ĺؼ���


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
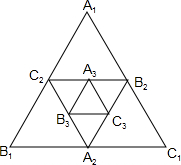 ��ͼ��Сǿ�����߳�Ϊ1�ĵ�1���ȱߡ�A1B1C1�����������ΪS1��Ȼ��ֱ�ȡ��A1B1C1���ߵ��е�A2��B2��C1��������2���ȱߡ�A2B2C2�����������ΪS2����ͬ���ķ�����������3���ȱߡ�A3B3C3�����������ΪS3�����˹��ɽ�����ȥ�������ɴ˿ɵã���20���ȱߡ�A20B20C20�����S20=$\frac{\sqrt{3}}{{4}^{20}}$��
��ͼ��Сǿ�����߳�Ϊ1�ĵ�1���ȱߡ�A1B1C1�����������ΪS1��Ȼ��ֱ�ȡ��A1B1C1���ߵ��е�A2��B2��C1��������2���ȱߡ�A2B2C2�����������ΪS2����ͬ���ķ�����������3���ȱߡ�A3B3C3�����������ΪS3�����˹��ɽ�����ȥ�������ɴ˿ɵã���20���ȱߡ�A20B20C20�����S20=$\frac{\sqrt{3}}{{4}^{20}}$���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
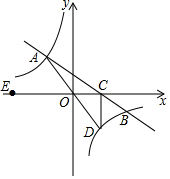 ��ͼ����ƽ��ֱ������ϵxOy�У�һ�κ���y=kx+b��ͼ���뷴��������y=$\frac{m}{x}$��m��0����ͼ���ڶ����������ڵ�A��B���㣬��x�ύ��C�㣬��B������Ϊ��12��n��
��ͼ����ƽ��ֱ������ϵxOy�У�һ�κ���y=kx+b��ͼ���뷴��������y=$\frac{m}{x}$��m��0����ͼ���ڶ����������ڵ�A��B���㣬��x�ύ��C�㣬��B������Ϊ��12��n���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
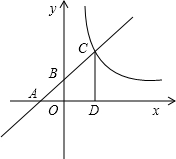 ��ͼ����֪һ�κ���y=kx+b��k��0����ͼ����x�ᡢy��Ľ���ֱ�ΪA��B���㣮���뷴��������y=$\frac{m}{x}$��m��0����ͼ���ڵ�һ�����ڵ�C��CD��ֱ��x�ᣬ����ΪD����OA=OB=OD=1��
��ͼ����֪һ�κ���y=kx+b��k��0����ͼ����x�ᡢy��Ľ���ֱ�ΪA��B���㣮���뷴��������y=$\frac{m}{x}$��m��0����ͼ���ڵ�һ�����ڵ�C��CD��ֱ��x�ᣬ����ΪD����OA=OB=OD=1���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
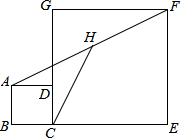 ��ͼ��������ABCD��������CEFG�У���D��CG�ϣ�BC=1��CE=4��H��AF���е㣬��ôCH�ij���$\frac{1}{2}\sqrt{34}$��
��ͼ��������ABCD��������CEFG�У���D��CG�ϣ�BC=1��CE=4��H��AF���е㣬��ôCH�ij���$\frac{1}{2}\sqrt{34}$���鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com