练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    9．已知cosα=0.8391，cotβ=0.5774，则锐角α，β的大小关系是（　　）
    A．α＞βB．α≤βC．α＜βD．α=β

    分析 根据余弦值随着角度的增大（或减小）而减小（或增大）可得答案．

    解答 解：∵cosα=0.8391，cotβ=0.5774，
    ∴α＜β，
    故选：C．

    点评 此题主要考查了锐角三角函数的增减性，关键是掌握①正弦值随着角度的增大（或减小）而增大（或减小）；②余弦值随着角度的增大（或减小）而减小（或增大）；③正切值随着角度的增大（或减小）而增大（或减小）．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

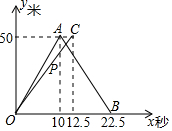    19．甲、乙两人在相邻两条直跑道上进行竞走比赛（注：跑道长50米，两人均往返一次，返回时转身的时间忽略不计），图中的折线OA-AB是甲离出发点的距离y（米）与比赛时间x（秒）的函数图象；线段OC是乙离出发点的距离y（米）与比赛时间x（秒）的函数图象，其中x≥0，线段OC与AB相交于点P．根据图象，解决下列问题：
    （1）求线段OC，AB对应的函数关系式，并写出相应的自变量x的取值范围；
    （2）直接写出点P的坐标，并说明点P的横、纵坐标的实际意义；
    （3）若乙往返时的速度相等且均为匀速运动，请在图中画出乙返回时的图象，并标明乙返回出发点的时间．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    20．下列各组数据分别是三角形的三边长，其中不能构成直角三角形的是（　　）
    A．2，4，2$\sqrt{3}$B．1，1，$\sqrt{2}$C．1，2，$\sqrt{5}$D．$\sqrt{3}$，2，$\sqrt{5}$

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    17．如图：点P是线段AB上任意一点，且C、D分别为线段AP、BP的中点，若CD=5cm，则有AB=10cm．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

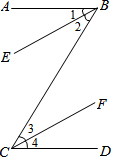    4．补全下题的证明过程（括号里面填依据）．
    已知：如图，AB∥CD，BE平分∠ABC，CF平分∠BCD，
    求证：BE∥CF
    证明：∵AB∥CD  （已知）
    ∴∠ABC=∠BCD（两直线平行，内错角相等）
    ∵BE平分∠ABC （已知）
    ∴∠2=$\frac{1}{2}$∠ABC角平分线的定义
    同理：∠3=$\frac{1}{2}$∠BCD
    ∴∠2=∠3等量代换
    ∴BE∥CF内错角相等，两直线平行．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    14．如图，AD是△ABC的中线，E是AD中点，BE的延长线与AC交于点F，则AF：AC等于（　　）
    A．1：2B．2：3C．1：3D．2：5

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    1．要使式子$\frac{4}{x-2}$有意义，则x的取值范围是（　　）
    A．x＞2B．x≥2C．x≠2D．x≠-2

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    18．下列各式中，最简二次根式是（　　）
    A．$\sqrt{\frac{1}{5}}$B．$\sqrt{7}$C．$\sqrt{24}$D．$\frac{1}{{\sqrt{2}}}$

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

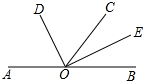    19．填空，完成下列说理过程：
    如图，点A，O，B在同一条直线上，OD，OE分别平分∠AOC和∠BOC．
    （1）求∠DOE的度数；
    （2）如果∠COD=65°，求∠AOE的度数．
    解：（1）如图，因为OD是∠AOC的平分线，所以∠COD=$\frac{1}{2}$∠AOC，又因为OE是∠BOC的平分线所以∠COE=$\frac{1}{2}$∠BOC．
    所以∠DOE=∠COD+∠COE=$\frac{1}{2}$（∠AOC+∠BOC）=$\frac{1}{2}$∠AOB=90°．
    （2）由（1）可知，∠BOE=∠COE=90°-∠COD=25°．所以∠AOE=∠AOB-∠BOE=155°．

    查看答案和解析>>

    同步练习册答案