
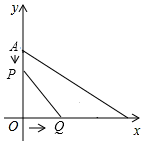 如图,在平面直角坐标系中,已知点A(0,6),B(8,0).点P从A点出发,以每秒1个单位的速度沿AO运动;同时,点Q从O出发,以每秒2个单位的速度沿OB运动,当Q点到达B点时,P、Q两点同时停止运动.
如图,在平面直角坐标系中,已知点A(0,6),B(8,0).点P从A点出发,以每秒1个单位的速度沿AO运动;同时,点Q从O出发,以每秒2个单位的速度沿OB运动,当Q点到达B点时,P、Q两点同时停止运动.分析 (1)由点Q从O出发,以每秒2个单位的速度沿OB运动,当Q点到达B点时,P、Q两点同时停止运动,可得:2t=8,解得:t=4,进而可得:0≤t≤4;
(2)分两种情况讨论:①Rt△POQ∽Rt△AOB;②Rt△QOP∽Rt△AOB,然后根据相似三角形对应边成比例,即可求出相应的t的值.
解答 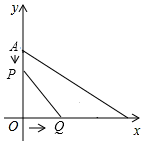 解:(1)∵点A(0,6),B(8,0),
解:(1)∵点A(0,6),B(8,0),
∴OA=6,OB=8,
∵点Q从O出发,以每秒2个单位的速度沿OB运动,当Q点到达B点时,P、Q两点同时停止运动,
∴2t=8,
解得:t=4,
∴0≤t≤4;
(2)①若Rt△POQ∽Rt△AOB时,
∵Rt△POQ∽Rt△AOB,
∴$\frac{PO}{AO}$=$\frac{OQ}{OB}$,
即$\frac{6-t}{6}$=$\frac{2t}{8}$,
解得:t=$\frac{12}{5}$;
②若Rt△QOP∽Rt△AOB时,
∵Rt△QOP∽Rt△AOB,
∴$\frac{OQ}{AO}$=$\frac{OP}{OB}$,
即$\frac{2t}{6}$=$\frac{6-t}{8}$,
解得:t=$\frac{18}{11}$.
所以当t为$\frac{12}{5}$或$\frac{18}{11}$时,Rt△POQ与Rt△AOB相似.
点评 此题是一次函数的综合题型,主要考查了三角形的面积,二次函数的最值,相似三角形的判定与性质,第(2)问的解题的关键是:分两种情况讨论:①Rt△POQ∽Rt△AOB;②Rt△QOP∽Rt△AOB.


 学而优暑期衔接南京大学出版社系列答案
学而优暑期衔接南京大学出版社系列答案 Happy holiday欢乐假期暑假作业广东人民出版社系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案 快乐暑假暑假能力自测中西书局系列答案
快乐暑假暑假能力自测中西书局系列答案科目:初中数学 来源: 题型:解答题
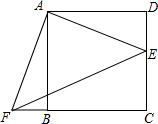 如图,点E是正方形ABCD的边DC上一点,把△ADE顺时针旋转△ABF的位置.
如图,点E是正方形ABCD的边DC上一点,把△ADE顺时针旋转△ABF的位置.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 图象必经过点(-1,2) | B. | y随x的增大而增大 | ||
| C. | 图象在第二、四象限内 | D. | 若y=1,则x=-2 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
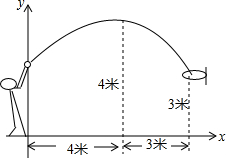 如图示:学校九年级的一场篮球比赛中,队员甲正在投篮,已知球出手时离地面高为$\frac{20}{9}$米,与篮筐中心的水平距离为7米,当球出手后球与队员甲的水平距离为4米时球达到最大高度4米,设篮球运行的轨迹为抛物线,篮筐距地面3米.
如图示:学校九年级的一场篮球比赛中,队员甲正在投篮,已知球出手时离地面高为$\frac{20}{9}$米,与篮筐中心的水平距离为7米,当球出手后球与队员甲的水平距离为4米时球达到最大高度4米,设篮球运行的轨迹为抛物线,篮筐距地面3米.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com