
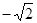 x2+mx+n的图象经过A,C两点.
x2+mx+n的图象经过A,C两点.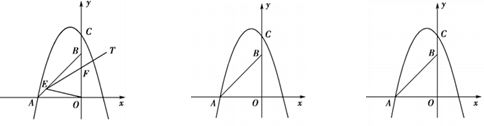
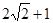 )倍.若存在,请直接写出点P坐标;若不存在,请说明理由.
)倍.若存在,请直接写出点P坐标;若不存在,请说明理由. x2-
x2- x+2
x+2 ;(2)证明见解析;(3)(-1, 1),(-
;(2)证明见解析;(3)(-1, 1),(- , 2-
, 2- );(4)P(0, 2
);(4)P(0, 2 )或P(-1,2
)或P(-1,2 )
) ∵OC=AB∴OC=2
∵OC=AB∴OC=2 , 即C (0,2
, 即C (0,2 )
) x2+mx+n的图象经过A、C两点 则可得
x2+mx+n的图象经过A、C两点 则可得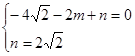 解得:
解得:
 x2-
x2- x+2
x+2
 OB=
OB= ×2=1 ∴ E(-1, 1)
×2=1 ∴ E(-1, 1)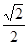 =
=
 ∴ E(-
∴ E(- , 2-
, 2- )
) , 2-
, 2-  )
) )或P (-1, 2
)或P (-1, 2  )
)


科目:初中数学 来源:不详 题型:解答题
 交坐标轴于A、B、D三点,过点D作
交坐标轴于A、B、D三点,过点D作 轴的平行线交抛物线于点C.直线l过点E(0,-
轴的平行线交抛物线于点C.直线l过点E(0,- ),且平分梯形ABCD面积.
),且平分梯形ABCD面积. ,求点P的坐标.
,求点P的坐标.
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
 =7.14,
=7.14, =7.21,
=7.21, =7.28,
=7.28,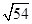 =7.35)
=7.35)
查看答案和解析>>
科目:初中数学 来源:不详 题型:填空题

查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
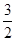 ),点M是抛物线C2:y=mx2-2mx-3m(m<0)的顶点.
),点M是抛物线C2:y=mx2-2mx-3m(m<0)的顶点.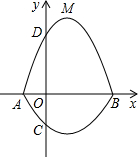
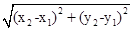 .
.查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
 与x轴交于点A、与y轴交于点D,以AD为腰,以x轴为底作等腰梯形ABCD(AB>CD),且等腰梯形的面积是8
与x轴交于点A、与y轴交于点D,以AD为腰,以x轴为底作等腰梯形ABCD(AB>CD),且等腰梯形的面积是8 ,抛物线经过等腰梯形的四个顶点.
,抛物线经过等腰梯形的四个顶点.
 轴的另一个交点为E,作EF⊥AD,垂足为F,请判断EF与⊙P的位置关系,并给以证明;
轴的另一个交点为E,作EF⊥AD,垂足为F,请判断EF与⊙P的位置关系,并给以证明;
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
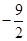 );Rt△ABC的直角边BC在x轴上,直角顶点C的坐标为(
);Rt△ABC的直角边BC在x轴上,直角顶点C的坐标为( ,0),且BC=5,AC=3(如图1).
,0),且BC=5,AC=3(如图1).
查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题
 的最小值”提出各自的想法.甲说:“可以利用已经学过的完全平方公式,把它配方成
的最小值”提出各自的想法.甲说:“可以利用已经学过的完全平方公式,把它配方成 ,所以代数式的最小值为-2”.乙说:“我也用配方法,但我配成
,所以代数式的最小值为-2”.乙说:“我也用配方法,但我配成 ,最小值为2”.你认为( )
,最小值为2”.你认为( )| A.甲对 | B.乙对 | C.甲、乙都对 | D.甲乙都不对 |
查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题

| A.(-3,0) | B.(-2,0) |
| C.x=-3 | D.x=-2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com