
【题目】如图,菱形ABCD中,AB=1,∠A=60°,EFGH是矩形,矩形的顶点都在菱形的边上.设AE=AH=x(0<x<1),矩形的面积为S.
(1)求S关于x的函数解析式;
(2)当EFGH是正方形时,求S的值.

【答案】(1)矩形EFGH的面积为S=-![]() x2+
x2+![]() x(0<x<1);(2)S=
x(0<x<1);(2)S=![]() .
.
【解析】
(1)连接BD交EF于点M,根据菱形的性质得出AB=AD,BD⊥EF,求出△AEH是等边三角形,根据等边三角形的性质得出∠AEH=∠ABD=60°,∠BEM=30°,BE=2BM,求出EM=![]() BE,即可求出答案;
BE,即可求出答案;
(2)根据正方形的性质求出x,再求出面积即可.
(1)连接BD交EF于点M,

∵四边形ABCD是菱形,
∴AB=AD,
∵AE=AH,
∴EH∥BD∥FG,BD⊥EF,
∵在菱形ABCD中,∠A=60°,AE=AH,
∴△AEH是等边三角形,
∴∠AEH=∠ABD=60°,∠BEM=30°,BE=2BM,
∴EM=![]() BE,
BE,
∴EF=![]() BE,
BE,
∵AB=1,AE=x,
∴矩形EFGH的面积为S=EH×EF=x×![]() (1-x)=-
(1-x)=-![]() x2+
x2+![]() x(0<x<1);
x(0<x<1);
(2)当矩形EFGH是正方形时,EH=EF,
即x=![]() (1-x),
(1-x),
解得:x=![]() ,
,
所以S=x2=(![]() )2=
)2=![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,直线y=kx+b经过点A(5,0),B(1,4).

(1)求直线AB的表达式;
(2)若直线y=2x-4与直线AB相交于点C,求点C的坐标;
(3)根据图象,写出关于x的不等式kx+b>2x-4>0的解集.
查看答案和解析>>
科目:初中数学 来源: 题型:
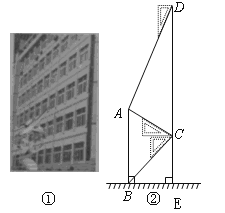
【题目】腾飞中学在教学楼前新建了一座“腾飞”雕塑(如图①).为了测量雕塑的高度,小明在二楼找到一点C,利用三角板测得雕塑顶端A点的仰角为![]() ,底部B点的俯角为
,底部B点的俯角为![]() ,小华在五楼找到一点D,利用三角板测得A点的俯角为
,小华在五楼找到一点D,利用三角板测得A点的俯角为![]() (如图②).若已知CD为10米,请求出雕塑AB的高度.(结果精确到0.1米,参考数据
(如图②).若已知CD为10米,请求出雕塑AB的高度.(结果精确到0.1米,参考数据![]() ).
).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为选拔一名选手参加“美丽江门,我为侨乡做代言”主题演讲比赛,经研究,按下图所示的项目和权数对选拔赛参赛选手进行考评(因排版原因统计图不完整).下表是李明、张华在选拔赛中的得分情况:
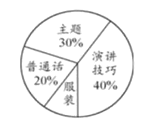
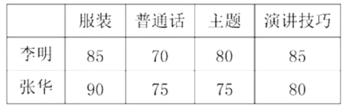
结合以上信息,回答下列问题:
(1)求服装项目在选手考评中的权数;
(2)根据你所学的知识,帮助学校在李明、张华两人中选择一人参加“美丽江门,我为侨乡做代言”主题演讲比赛,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+bx+c的图象经过点A(﹣2,0),点B(4,0),点D(2,4),与y轴交于点C,作直线BC,连接AC,CD.

(1)求抛物线的函数表达式;
(2)E是抛物线上的点,求满足∠ECD=∠ACO的点E的坐标;
(3)点M在y轴上且位于点C上方,点N在直线BC上,点P为第一象限内抛物线上一点,若以点C,M,N,P为顶点的四边形是菱形,求菱形的边长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面材料:
在数学课上,老师提出如下问题:
尺规作图:作一条线段的垂直平分线.
已知:线段AB.
求作:线段AB的垂直平分线.
小红的作法如下:
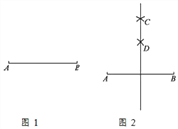
如图,①分别以点A和点B为圆心,大于![]() AB的长为半径作弧,两弧相交于点C;
AB的长为半径作弧,两弧相交于点C;
②再分别以点A和点B为圆心,大于![]() AB的长为半径(不同于①中的半径)作弧,两弧相交于点D,使点D与点C在直线AB的同侧;
AB的长为半径(不同于①中的半径)作弧,两弧相交于点D,使点D与点C在直线AB的同侧;
③作直线CD.
所以直线CD就是所求作的垂直平分线.
老师说:“小红的作法正确.”
请回答:小红的作图依据是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】古希腊著名的毕达哥拉斯学派把1,3,6,10…这样的数称为“三角形数”,而把1,4,9,16…这样的数称为“正方形数”.从图中可以发现,任何一个大于1的“正方形数”都可以看作两个相邻“三角形数”之和.下列等式中,符合这一规律的是( )
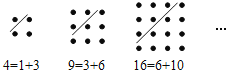
A. 36=15+21 B. 25=9+16 C. 13=3+10 D. 49=18+31
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】关于函数y=﹣2x+1,下列结论正确的是( )
A. 图象必经过点(﹣2,1) B. 图象经过第一、二、三象限
C. 当x>![]() 时,y<0 D. y随x的增大而增大
时,y<0 D. y随x的增大而增大
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com