
分析 先作辅助线,构建平行四边形和梯形的高线,设EG=x,AM=h1,MN=h2,因为EG∥DH得△AEG∽△ADH,根据相似三角形对应边的比等于对应高的比得$\frac{EG}{DH}=\frac{AM}{AN}$,代入求出$\frac{{h}_{1}}{{h}_{2}}$=$\frac{x}{b-a-x}$,再由已知的S梯形ABFE:S梯形EFCD=m:n代入得:(m+n)EF2=a2n+b2m,解方程即可.
解答 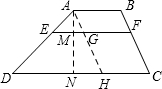 解:过A作AH∥BC,交DC于H,交EF于G,得?AGFB、?GHCF,
解:过A作AH∥BC,交DC于H,交EF于G,得?AGFB、?GHCF,
∴FG=HC=AB=a,
过A作AN⊥DC于N,交EF于M,则AN⊥EF,
设EG=x,AM=h1,MN=h2,
∵EG∥DH,
∴△AEG∽△ADH,
∴$\frac{EG}{DH}=\frac{AM}{AN}$,
∴$\frac{x}{b-a}=\frac{{h}_{1}}{{h}_{1}+{h}_{2}}$,
∴$\frac{{h}_{1}}{{h}_{2}}$=$\frac{x}{b-a-x}$,
∵S梯形ABFE:S梯形EFCD=m:n,
∴$\frac{\frac{1}{2}(AB+EF)•{h}_{1}}{\frac{1}{2}(DC+EF)•{h}_{2}}$=$\frac{m}{n}$,
∴$\frac{AB+EF}{DC+EF}$•$\frac{x}{b-a-x}$=$\frac{m}{n}$,
∴$\frac{(a+EF)(EF-a)}{(b+EF)(b-EF)}$=$\frac{m}{n}$,
(m+n)EF2=a2n+b2m,
∵EF>0,
∴EF=$\sqrt{\frac{m{b}^{2}+n{a}^{2}}{m+n}}$=$\frac{\sqrt{(m+n)(m{b}^{2}+n{a}^{2})}}{m+n}$.
故答案为:$\frac{\sqrt{(m+n)(m{b}^{2}+n{a}^{2})}}{m+n}$.
点评 此题考查了梯形、平行四边形以及相似三角形的判定与性质,注意准确作出辅助线是解此题的关键;巧妙的设未知数,表示其它边的长度,代入S梯形ABFE:S梯形EFCD=m:n中,即可得出结论.


科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,CD分别交AD,EG于点D,G,EB分别交AD,EG于点A,E,AC交EG于点F,FH交AD于点H,AD平分∠BAC,EG∥AD,CG⊥EG,∠C=∠AFH.
如图,CD分别交AD,EG于点D,G,EB分别交AD,EG于点A,E,AC交EG于点F,FH交AD于点H,AD平分∠BAC,EG∥AD,CG⊥EG,∠C=∠AFH.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com