
����Ŀ��Ϊ�˽�������������������ɫ��������ʽ�������ij������ѧ��ȤС�����ʾ��������ʽ����������˱�У����ѧ������ѧ����Ҫ���з�ʽ��������������������ͼ��ʾ��������������ͳ��ͼ�������ͼ���ṩ����Ϣ����������⣺
���� |
|
|
|
|
|
���з�ʽ | ���� | ������ | ���г� | ˽�ҳ� | ��� |
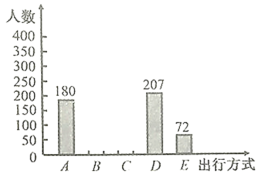
��1�����뱾���ʾ������ѧ������_________�ˣ�����ѡ��![]() ���������ռ�İٷֱ�Ϊ____________��
���������ռ�İٷֱ�Ϊ____________��
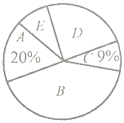
��2����ͨ�����㲹ȫ����ͳ��ͼ������������ͳ��ͼ��![]() ������Ӧ���ε�Բ�ĽǵĶ�����
������Ӧ���ε�Բ�ĽǵĶ�����
��3����������������ÿ��Լ![]() �˳��У�����
�˳��У�����![]() ��
��![]() ��
��![]() ��������з�ʽ����Ϊ����ɫ��������ʽ���������������������ѡȡ����ɫ��������ʽ��������
��������з�ʽ����Ϊ����ɫ��������ʽ���������������������ѡȡ����ɫ��������ʽ��������
���𰸡���1��900��23������2����������144�㣻��3����������������ѡȡ����ɫ��������ʽ������Ϊ13110��
��������
��1������A�����������ռ�İٷֱ����������������D��������������������Եó�D���������ռ�İٷֱȣ�
��2����������������C���������ռ�İٷֱȿ��Եó�C����������Ӷ��ó�B������������ɲ�ȫ����ͳ��ͼ��������B��������������������Եó�B���������ռ�İٷֱȣ������������B������Ӧ��Բ�ĽǵĶ�����
��3�������������������˼�������⼴�ɣ�
�⣺��1��180��20%=900���ˣ���207��900=23����
�ʴ�Ϊ��900��23%��
��2��C���������900��9��=81���ˣ���B���������900-180-81-207-72=360���ˣ���
��ȫͳ��ͼ���£�

B���������ռ�ٷֱ�Ϊ��![]() 100%=40%��
100%=40%��
B�����������Ӧ���ε�Բ�ĽǵĶ���Ϊ��360���40%=144�㣻
��3����������ã�19000����20��+40��+9����=13110���ˣ���
����������������ѡȡ����ɫ��������ʽ������ԼΪ13110�ˣ�


 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
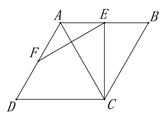
����Ŀ����ͼ���ı���ABCD�DZ߳�Ϊ2�����Σ�E��F�ֱ���AB��AD���е㣬����EF��EC������FAE�Ƶ�F��ת180���õ���FDM��
(1)��ȫͼ�β�֤����EF��AC��
(2)����B=60��������EMC�������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
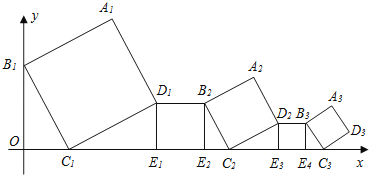
����Ŀ��һ�������ΰ���ͼ��ʾ�ķ�ʽ���ã����ж���B1��y���ϣ�����C1��E1��E2��C2��E3��E4��C3����x���ϣ���֪������A1B1C1D1�ı߳�Ϊ1����B1C1O��60�㣬B1C1��B2C2��B3C3����������A2017B2017C2017D2017�ı߳��ǣ�������
A. ��![]() ��2016 B. ��
��2016 B. ��![]() ��2017 C. ��
��2017 C. ��![]() ��2016 D. ��
��2016 D. ��![]() ��2017
��2017
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
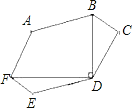
����Ŀ����ͼ��ʾ������ABCDEF�У�ABƽ���ҵ���ED��AFƽ���ҵ���CD��BCƽ���ҵ���FE���Խ���FD��BD����֪FD��24![]() ��BD��18
��BD��18![]() ����������ABCDEF�������______.
����������ABCDEF�������______.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��A����2��1����B��1��4����������������y=![]() ���߶�AB�й�����ʱ��k��ȡֵ��Χ�ǣ�������
���߶�AB�й�����ʱ��k��ȡֵ��Χ�ǣ�������
A. ��![]() ��k��0��0��k��4 B. k����2��k��4
��k��0��0��k��4 B. k����2��k��4
C. ��2��k��0��k��4 D. ��2��k��0��0��k��4
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪![]() ���������������ֱ�Ϊ
���������������ֱ�Ϊ![]() ��
��![]() ��
��![]() .
.
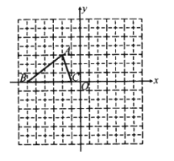
��1����ֱ��д����![]() ����ԭ��ԳƵĵ�����ꣻ
����ԭ��ԳƵĵ�����ꣻ
��2����![]() ������ԭ��
������ԭ��![]() ��ʱ����ת
��ʱ����ת![]() �õ�
�õ�![]() ������
������![]() ��ֱ��д����
��ֱ��д����![]() ��
��![]() �Ķ�Ӧ��ĵ�
�Ķ�Ӧ��ĵ�![]() ��
��![]() ���ꣻ
���ꣻ
��3����ֱ��д������![]() ��
��![]() ��
��![]() Ϊ�����ƽ���ı��εĵ��ĸ�����
Ϊ�����ƽ���ı��εĵ��ĸ�����![]() ������.
������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
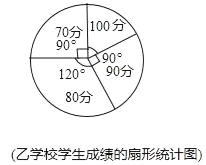
����Ŀ������ѧ��������չʾ��У�ij�ؽ����־����ڼס�����У������ѧ����������������涨�ס�����ѧУѡ����ͬ������ѡ�ֲμӣ������������ֲ���ѡ�ֵijɼ���70�֡�80�֡�90�֡�l00�������ֳɼ��е�һ�֣���֪�ס�����У��ѡ�ֻ��100�ֵ�������ȣ��ָ��ݼס�����Уѡ�ֵijɼ������Ƴ�����������ͳ��ͼ���£�
��1���벹ȫ����ͳ��ͼ��
��2���������������־����Լס�����У���100�ֵ�ѡ�ֽ��м�����ѵ����ѵ�������ѡȡ��λѡ�ֲμ�����ľ����������б�������״ͼ�ķ���������ѡ��λѡ������ͬһѧУ�ĸ��ʣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ABCD�У�E��AD���е㣬�ӳ�CE��BA���ڵ�F������AC��DF��
��1����֤���ı���ACDF��ƽ���ı��Σ�
��2����CFƽ�֡�BCDʱ��д��BC��CD��������ϵ����˵�����ɣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ֱ��AB,CD���ڵ�O��OEƽ��![]() ��OF��
��OF��![]() �Ľ�ƽ���ߣ�
�Ľ�ƽ���ߣ�
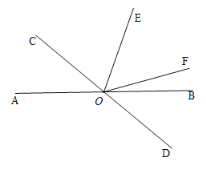
��1��˵��: ![]() ��
��
��2����![]() ����
����![]() �Ķ�����
�Ķ�����
��3����![]() ����
����![]() �Ķ�����
�Ķ�����
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com