
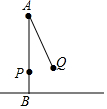
 如图,旗杆AB顶端系一根绳子AP,绳子底端离地面的距离为1m,小明将绳子拉到AQ的位置,测得∠PAQ=25°,此时点Q离地面的高度为1.5m,求旗杆的高度(结果保留整数.sin25°=0.42,cos25°=0.90,tan25°=0.47)
如图,旗杆AB顶端系一根绳子AP,绳子底端离地面的距离为1m,小明将绳子拉到AQ的位置,测得∠PAQ=25°,此时点Q离地面的高度为1.5m,求旗杆的高度(结果保留整数.sin25°=0.42,cos25°=0.90,tan25°=0.47)  七彩题卡口算应用一点通系列答案
七彩题卡口算应用一点通系列答案科目:初中数学 来源: 题型:选择题
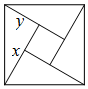 如图,是4个全等的直角三角形镶嵌而成的正方形图案,已知大正方形的面积为49,小正方形的面积为4,若用x,y表示直角三角形的两条直角边(x>y),请观察图案,指出下列关系式不正确的是( )
如图,是4个全等的直角三角形镶嵌而成的正方形图案,已知大正方形的面积为49,小正方形的面积为4,若用x,y表示直角三角形的两条直角边(x>y),请观察图案,指出下列关系式不正确的是( )| A. | x2+y2=49 | B. | x-y=2 | C. | 2xy+4=49 | D. | x+y=13 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
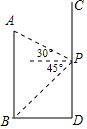 如图,AB、CD分别表示两幢相距36米的大楼,小明同学站在CD大楼的P处窗口观察AB大楼的底部B点的俯角为45°,观察AB大楼的顶部A点的仰角为30°.
如图,AB、CD分别表示两幢相距36米的大楼,小明同学站在CD大楼的P处窗口观察AB大楼的底部B点的俯角为45°,观察AB大楼的顶部A点的仰角为30°.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
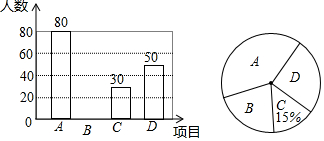
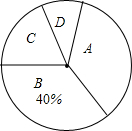 2017年2月8日晚,央视一套播出感动中国2016年度人物颁奖盛典,三入火海救人的南阳人王峰的当选,在中原大地引起强烈反响,社会各界纷纷表达对英雄的敬意,厚重的历史文化,历代先贤的故事,层出不穷的“河南好人”潜移默化地影响着中原儿女,为了弘扬中原优秀传统文化,某中学举办了中原文化知识大赛,并随机抽取了50名学生的成绩(得分为整数),将他们的得分按优秀、良好、及格、不及格(分别用A,B,C,D表示)四个等级进行统计,并绘制成下面的统计表和扇形统计图:
2017年2月8日晚,央视一套播出感动中国2016年度人物颁奖盛典,三入火海救人的南阳人王峰的当选,在中原大地引起强烈反响,社会各界纷纷表达对英雄的敬意,厚重的历史文化,历代先贤的故事,层出不穷的“河南好人”潜移默化地影响着中原儿女,为了弘扬中原优秀传统文化,某中学举办了中原文化知识大赛,并随机抽取了50名学生的成绩(得分为整数),将他们的得分按优秀、良好、及格、不及格(分别用A,B,C,D表示)四个等级进行统计,并绘制成下面的统计表和扇形统计图:| 等级 | 成绩(分) | 频数(人数) | 频率 |
| A | 90~100 | 19 | 0.38 |
| B | 75~89 | m | x |
| C | 60~74 | n | y |
| D | 60以下 | 3 | 0.06 |
| 合计 | 50 | 1.00 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
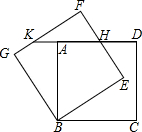 如图,正方形ABCD绕点B逆时针旋转30°后得到正方形BEFG,EF与AD相交于点H,延长DA交GF于点K.若正方形ABCD边长为$\sqrt{3}$,则HD的长为$\sqrt{3}$-1.
如图,正方形ABCD绕点B逆时针旋转30°后得到正方形BEFG,EF与AD相交于点H,延长DA交GF于点K.若正方形ABCD边长为$\sqrt{3}$,则HD的长为$\sqrt{3}$-1.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
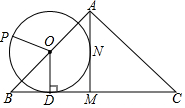 如图,在△ABC中,AB=AC,点O为边AB的中点,OD⊥BC于点D,AM⊥BC于点M,以点O为圆心,线段OD为半径的圆与AM相切于点N.
如图,在△ABC中,AB=AC,点O为边AB的中点,OD⊥BC于点D,AM⊥BC于点M,以点O为圆心,线段OD为半径的圆与AM相切于点N.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com