
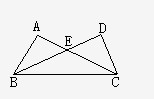
 9、如图,∠A,∠D为直角,BE=EC,则图中全等的两对三角形可以是
9、如图,∠A,∠D为直角,BE=EC,则图中全等的两对三角形可以是科目:初中数学 来源: 题型:
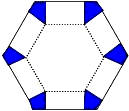 如图,将边长为6cm的正六边形纸板的六个角各剪切去一个全等的四边形,再沿虚线折起,做成一个无盖直六棱柱纸盒,使侧面积等于底面积,被剪去的六个四边形的面积和为
如图,将边长为6cm的正六边形纸板的六个角各剪切去一个全等的四边形,再沿虚线折起,做成一个无盖直六棱柱纸盒,使侧面积等于底面积,被剪去的六个四边形的面积和为查看答案和解析>>
科目:初中数学 来源: 题型:
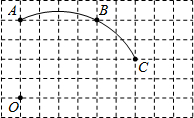 如图,在单位长度为1的正方形网格中,一段圆弧经过网格的交点A、B、C.
如图,在单位长度为1的正方形网格中,一段圆弧经过网格的交点A、B、C.查看答案和解析>>
科目:初中数学 来源: 题型:
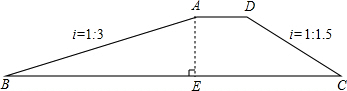 坡AB的坡度i=1:3(指坡面的铅直高度AE与水平宽度BE的比),斜坡DC的坡度i=1:1.5,已知该拦水坝的高为6米.
坡AB的坡度i=1:3(指坡面的铅直高度AE与水平宽度BE的比),斜坡DC的坡度i=1:1.5,已知该拦水坝的高为6米.查看答案和解析>>
科目:初中数学 来源: 题型:
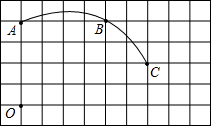 系;②用直尺和圆规画出该圆弧所在圆的圆心D的位置(不用写作法,保留作图痕迹),并连接AD、CD.
系;②用直尺和圆规画出该圆弧所在圆的圆心D的位置(不用写作法,保留作图痕迹),并连接AD、CD.| 5 |
| 5 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com