
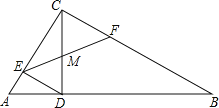
【题目】已知△ABC中,∠ACB=90°,AC=3,tanA=![]() ,CD⊥AB于点D,DE⊥AC,点F在线段BC上,EF交CD于点M.
,CD⊥AB于点D,DE⊥AC,点F在线段BC上,EF交CD于点M.

(1)求CD的长;
(2)若△EFC与△ABC相似,试求线段EM的长.
【答案】(1)2.4(2)![]() 或
或![]()
【解析】
试题分析:(1)由已知条件易求BC、AB的长,再根据△ACB的面积为定值即可求出CD的长,
(2)若△EFC与△ABC相似,则CE可以和BC为对应边,也可以和AC为对应边,所以此题要分两种情况讨论求出CF的长,再由△DEM∽△CFM即可求出不同情况下EM的长.
解:(1)∵∠ACB=90°,AC=3,tanA=![]() ,
,
∴BC=4,
∴AB=![]() =5,
=5,
∵CD⊥AB于点D,
∴![]() AC×BC=
AC×BC=![]() AB×CD,
AB×CD,
∴CD=2.4;
(2)∵CD⊥AB于点D,tanA=![]() ,AC=3,
,AC=3,
∴AD=![]() ,
,
∵DE⊥AC,tanA=![]() ,
,
∴AE=![]() ,DE=
,DE=![]() ,
,
∴CE=3﹣![]() =
=![]() ,
,
若△EFC与△ABC相似,
则![]() 或
或![]() ,
,
解得:CF=![]() 或
或![]() ,EF=
,EF=![]() 或
或![]() ,
,
∵DE⊥AC,BC⊥AC,
∴△DEM∽△CFM,
∴![]() ,
,
∴EM=![]() 或
或![]() .
.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD的对角线相交于点O,PB∥AC,PC∥BD,PB、PC相交于点P.

(1)猜想四边形PCOB是什么四边形,并说明理由;
(2)当矩形ABCD满足什么条件时,四边形PCOB是正方形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】兴发服装店老板用4500元购进一批某款T恤衫,由于深受顾客喜爱,很快售完,老板又用4950元购进第二批该款式T恤衫,所购数量与第一批相同,但每件进价比第一批多了9元.
(1)第一批该款式T恤衫每件进价是多少元?
(2)老板以每件120元的价格销售该款式T恤衫,当第二批T恤衫售出![]() 时,出现了滞销,于是决定降价促销,若要使第二批的销售利润不低于650元,剩余的T恤衫每件售价至少要多少元?(利润=售价﹣进价)
时,出现了滞销,于是决定降价促销,若要使第二批的销售利润不低于650元,剩余的T恤衫每件售价至少要多少元?(利润=售价﹣进价)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,已知点E在正方形ABCD的边BC上,若∠AEF=90°,且EF交正方形外角的平分线CF于点F.

(1)图1中若点E是边BC的中点,我们可以构造两个三角形全等来证明AE=EF,请叙述你的一个构造方案,并指出是哪两个三角形全等(不要求证明);
(2)如图2,若点E在线段BC上滑动(不与点B,C重合).
①AE=EF是否总成立?请给出证明;
②在图2的AB边上是否存在一点M,使得四边形DMEF是平行四边形?若存在,请给予证明;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】把下列各数分类
﹣3,0.45, ![]() ,0,9,﹣1,﹣1
,0,9,﹣1,﹣1![]() ,10,﹣3.14
,10,﹣3.14
(1)正整数:{ …}
(2)负整数:{ …}
(3)整数:{ …}
(4)分数:{ …}.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com