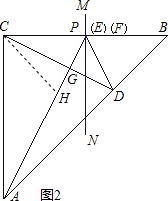

解:(1)如图2,AP=a+b;
(2)证明:如图3,作∠ACB的角平分线交AP于H,
∵∠ACB=90°
∴∠BCH=∠ACH=45°
在Rt△ABC中
∵BC=AC
∴∠B=45°
又∵P为BC的中垂线MN上一点,E,F关于MN对称
∴CE=BF,PE=PF
∴∠PEF=∠PFE
∴∠CEH=∠BFD
∴△CEH≌△BFD
∴CH=BD
∴△ACH≌△CBD
∴∠BCD=∠CAH
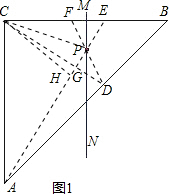
∵∠CAE+∠CEA=90°
∴∠GCE+∠CEG=90°
∴∠CGH=90°
∴CD⊥AE;
(3)如图1,AE=CD+DF.
分析:(1)可通过构建全等三角形得出角相等来求证.要证AP=CD+PD,那么就要证出PH=PD,AH=CD,那么可构建与三角形BCD全等的三角形来求解.过C作∠BCA的平分线交AP于H,那么就是证三角形ACH和BDC全等,已知AC=BC,∠ACH=∠B=45°,只要证出CH=BD就能得出两三角形全等,那么我们可通过全等三角形CHE和BDF来求证.E,F重合,MN垂直平分BC,那么CP=PB,∠CPH=90-∠HPN=90°-∠NPD=∠DPB,而∠HCB=∠B=45°,由此可得出两三角形全等,也就得出了CH=BD,PH=PD进而得出AH=CD,这样就能得出AE=AH+PH=CD+PD=a+b;
(2)可通过构建全等三角形得出角相等来求证.要证CG⊥AP,那么就要证出∠BCD=∠CAH,那么可构建与三角形BCD全等的三角形来求解.过C作∠BCA的平分线交AP于H,那么就是证三角形ACH和BDC全等,已知AC=BC,∠ACH=∠B=45°,只要证出CH=BD就能得出两三角形全等,那么我们可通过全等三角形CHE和BDF来求证.由于E,F关于MN对称,那么CE=BF,PE=PF,可得出∠PEF=∠PFE,也就是∠CEH=∠DFB,又已知了∠HCB=∠B=45°,因此就能得出三角形CEH与DFB全等,就能得出CH=BD,也就能得出三角形AHC与三角形BDC全等了.进而可通过∠DCB=∠CAG来得出CG⊥AP;
(3)方法同(1)完全一样.
点评:本题主要考查了对称的性质,等腰直角三角形的性质以及全等三角形的判定等知识点,根据已知和所求的条件构建出全等三角形是解题的关键.

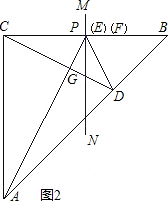


 解:(1)如图2,AP=a+b;
解:(1)如图2,AP=a+b;

