
【题目】某农科所甲、乙试验田各有水稻3万个,为了考察水稻穗长的情况,于同一天在这两块试验田里分别随机抽取了![]() 个稻穗进行测量,获得了它们的长度
个稻穗进行测量,获得了它们的长度![]() (单位:cm),并对数据(穗长)进行了整理、描述和分析.下面给出了部分信息.
(单位:cm),并对数据(穗长)进行了整理、描述和分析.下面给出了部分信息.
a.甲试验田穗长的频数分布统计表如下表所示(不完整):
甲试验田穗长频数分布表
分组/ | 频数 | 频率 |
| 4 | 0.08 |
| 9 | 0.18 |
|
| |
| 11 | 0.22 |
|
| 0.20 |
| 2 | |
合计 | 50 | 1.00 |
b.乙试验田穗长的频数分布直方图如图所示:
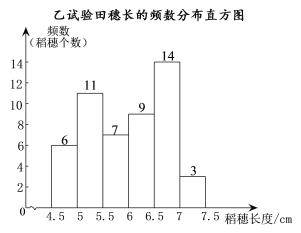
c.乙试验田穗长在![]() 这一组的是:
这一组的是:
6.3 6.4 6.3 6.3 6.2 6.2 6.1 6.2 6.4
d.甲、乙试验田穗长的平均数、中位数、众数、方差如下(表2):
试验田 | 平均数 | 中位数 | 众数 | 方差 |
甲 | 5.924 | 5.8 | 5.8 | 0.454 |
乙 | 5.924 |
| 6.5 | 0.608 |
根据以上信息,回答下列问题:
(1)表中![]() 的值为 ,
的值为 ,![]() 的值为 ;
的值为 ;
(2)表中![]() 的值为 ;
的值为 ;
(3)在此次考察中,稻穗生长(长度)较稳定的试验田是 ;
A.甲 B.乙 C.无法推断
(4)若穗长在![]() 范围内的稻穗为“良好”,请估计甲试验田所有“良好”的水稻约为 万个.
范围内的稻穗为“良好”,请估计甲试验田所有“良好”的水稻约为 万个.
【答案】(1)![]() ;
;![]() ;(2)
;(2)![]() ;(3)A;A;(4)
;(3)A;A;(4)![]() .
.
【解析】
(1)根据“频率=![]() ”求解即可;
”求解即可;
(2)根据中位数的定义求解即可;
(3)由于平均数相同,比较方差大小即可得出结论;
(4)先求出样本中“良好”所占百分数,再乘以总数即可.
(1)m=50×0.20=10;
2÷50=0.04,
n=1-0.04-0.20-0.22-0.18-0.08=0.28.
(2)样本共有50个数据,按大小顺序排列第25、26个数是最中间的两个数,
而第25、26个数是6.1和6.2,
因此,中位数是![]() (cm).
(cm).
(3)∵甲试验田穗长的方差小于乙试验田穗长的方差,
故选A.
(4)穗长在![]() 范围内的稻穗数为50-(4+9+2)=35,
范围内的稻穗数为50-(4+9+2)=35,
30000×![]() =21000=2.1万.
=21000=2.1万.
所以,甲试验田所有“良好”的水稻约为2.1万个.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
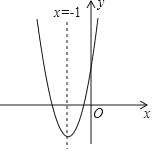
【题目】如图,抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=﹣1,给出下列结论:
①b2=4ac;②abc>0;③a>c; ④4a﹣2b+c>0,其中正确有_____(填序号).
查看答案和解析>>
科目:初中数学 来源: 题型:
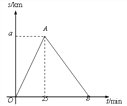
【题目】某市举行长跑比赛,运动员从甲地出发跑到乙地后,又沿原路线跑回起点甲地.如图是某运 动员离开甲地的路程 s(km)与跑步时间 t(min)之间的函数关系(OA、OB 均为线段).已 知该运动员从甲地跑到乙地时的平均速度是 0.2 km/min,根据图像提供的信息,解答下列问 题:
(1)a= km;
(2)组委会在距离起点甲地 3 km 处设立了一个拍摄点 P,该运动员从第一次过 P 点到第二
次过 P 点所用的时间为 24 min.
①求 AB 所在直线的函数表达式;
②该运动员跑完全程用时多少 min?
查看答案和解析>>
科目:初中数学 来源: 题型:
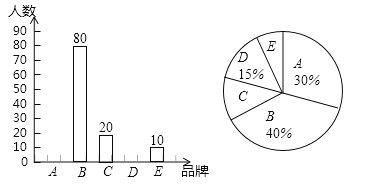
【题目】“共享单车,绿色出行”,现如今骑共享单车出行不但成为一种时尚,也称为共享经济的一种新形态,某校九(1)班同学在街头随机调查了一些骑共享单车出行的市民,并将他们对各种品牌单车的选择情况绘制成如下两个不完整的统计图(A:摩拜单车;B:ofo单车;C:HelloBike).请根据图中提供的信息,解答下列问题:
(1)求出本次参与调查的市民人数;
(2)将上面的条形图补充完整;
(3)若某区有10000名市民骑共享单车出行,根据调查数据估计该区有多少名市民选择骑摩托单车出行?
查看答案和解析>>
科目:初中数学 来源: 题型:
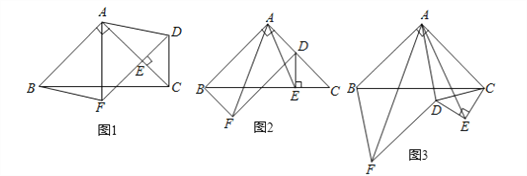
【题目】如图1,在等腰Rt△ABC中,∠BAC=90°,点E在AC上(且不与点A、C重合).在△ABC的外部作等腰Rt△CED,使∠CED=90°,连接AD,分别以AB,AD为邻边作平行四边形ABFD,连接AF.
(1)求证:△AEF是等腰直角三角形;
(2)如图2,将△CED绕点C逆时针旋转,当点E在线段BC上时,连接AE,求证:AF=![]() AE;
AE;
(3)如图3,将△CED绕点C继续逆时针旋转,当平行四边形ABFD为菱形,且△CED在△ABC的下方时,若AB=2![]() ,CE=2,求线段AE的长.
,CE=2,求线段AE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
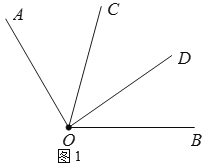
【题目】已知![]() (本题中的角均大于
(本题中的角均大于![]() 且小于
且小于![]() )
)
(1)如图1,在![]() 内部作
内部作![]() ,若
,若![]() ,求
,求![]() 的度数;
的度数;
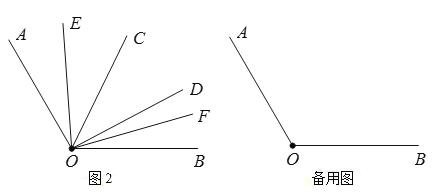
(2)如图2,在![]() 内部作
内部作![]() ,
,![]() 在
在![]() 内,
内,![]() 在
在![]() 内,且
内,且![]() ,
,![]() ,
,![]() ,求
,求![]() 的度数;
的度数;
(3)射线![]() 从
从![]() 的位置出发绕点
的位置出发绕点![]() 顺时针以每秒
顺时针以每秒![]() 的速度旋转,时间为
的速度旋转,时间为![]() 秒(
秒(![]() 且
且![]() ).射线
).射线![]() 平分
平分![]() ,射线
,射线![]() 平分
平分![]() ,射线
,射线![]() 平分
平分![]() .若
.若![]() ,则
,则![]() 秒.
秒.
查看答案和解析>>
科目:初中数学 来源: 题型:
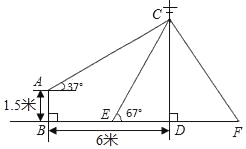
【题目】如图,在电线杆CD处引拉线CE,CF固定电线杆,拉线CE和地面所成的角∠CED=67°,在离电线杆6米的B处安置高为1.5米的测角仪AB,在A处测得电线杆上C处的仰角为37°,求拉线CE的长(参考数据:sin67°≈![]() ,cos67°≈
,cos67°≈![]() ,tan67°≈
,tan67°≈![]() ,sin37°≈
,sin37°≈![]() ,cos37°≈
,cos37°≈![]() ,tsn37°≈
,tsn37°≈![]() ).
).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】材料一:一个正整数x能写成x=a2﹣b2(a,b均为正整数,且a≠b),则称x为“雪松数”,a,b为x的一个平方差分解,在x的所有平方差分解中,若a2+b2最大,则称a,b为x的最佳平方差分解,此时F(x)=a2+b2.
例如:24=72﹣52,24为雪松数,7和5为24的一个平方差分解,32=92﹣72,32=62﹣22,因为92+72>62+22,所以9和7为32的最佳平方差分解,F(32)=92+72
材料二:若一个四位正整数,它的千位数字与个位数字相同,百位数字与十位数字相同,但四个数字不全相同,则称这个四位数为“南麓数”.例如4334,5665均为“南麓数”.
根据材料回答:
(1)请直接写出两个雪松数,并分别写出它们的一对平方差分解;
(2)试证明10不是雪松数;
(3)若一个数t既是“雪松数”又是“南麓数”,并且另一个“南麓数”的前两位数字组成的两位数与后两位数字组成的两位数恰好是t的一个平方差分解,请求出所有满足条件的数t中F(t)的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com