
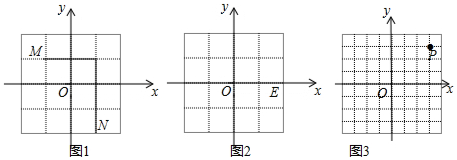
分析 【应用】:(1)根据若y1=y2,则AB∥x轴,且线段AB的长度为|x1-x2|,代入数据即可得出结论;
(2)由CD∥y轴,可设点D的坐标为(1,m),根据CD=2即可得出|0-m|=2,解之即可得出结论;
【拓展】:(1)根据两点之间的折线距离公式,代入数据即可得出结论;
(2)根据两点之间的折线距离公式结合d(E,H)=3,即可得出关于t的含绝对值符号的一元一次方程,解之即可得出结论;
(3)由点Q在x轴上,可设点Q的坐标为(x,0),根据三角形的面积公式结合三角形OPQ的面积为3即可求出x的值,再利用两点之间的折线距离公式即可得出结论.
解答 解:【应用】:
(1)AB的长度为|-1-2|=3.
故答案为:3.
(2)由CD∥y轴,可设点D的坐标为(1,m),
∵CD=2,
∴|0-m|=2,解得:m=±2,
∴点D的坐标为(1,2)或(1,-2).
故答案为:(1,2)或(1,-2).
【拓展】:
(1)d(E,F)=|2-(-1)|+|0-(-2)|=5.
故答案为:=5.
(2)∵E(2,0),H(1,t),d(E,H)=3,
∴|2-1|+|0-t|=3,解得:t=±2.
故答案为:2或-2.
(3)由点Q在x轴上,可设点Q的坐标为(x,0),
∵三角形OPQ的面积为3,
∴$\frac{1}{2}$|x|×3=3,解得:x=±2.
当点Q的坐标为(2,0)时,d(P,Q)=|3-2|+|3-0|=4;
当点Q的坐标为(-2,0)时,d(P,Q)=|3-(-2)|+|3-0|=8.
故答案为:4或8.
点评 本题考查了两点间的距离公式,读懂题意并熟练运用两点间的距离及两点之间的折线距离公式是解题的关键.


科目:初中数学 来源: 题型:解答题
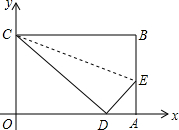 如图,四边形OABC是一张放在平面直角坐标系中的矩形纸片,点A在x轴上,点C在y轴上,将边BC折叠,使点B落在边OA的点D处.已知折痕CE=5$\sqrt{5}$,
如图,四边形OABC是一张放在平面直角坐标系中的矩形纸片,点A在x轴上,点C在y轴上,将边BC折叠,使点B落在边OA的点D处.已知折痕CE=5$\sqrt{5}$,查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com