练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    6．如图，AB∥CD，直线EF分别交AB、CD于点E、F，CE平分∠AEF，DE⊥CE，若∠ECF=42°，则∠FED=48°．

    分析 根据平行线的性质得到∠AEC=∠ECF，根据角平分线的定义得到CE平分∠AEF，等量代换得到∠AEC=∠CEF，根据垂线的定义即可得到结论．

    解答 解：∵AB∥CD，
    ∴∠AEC=∠ECF，
    ∵CE平分∠AEF，
    ∴∠AEC=∠CEF，
    ∴∠CEF=∠ECF=42°，
    ∵DE⊥CE，
    ∴∠FED=48°，
    故答案为：48．

    点评 本题考查了平行线性质：两直线平行，同位角相等；两直线平行，同旁内角互补；两直线平行，内错角相等．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：选择题

    16．二元一次方程x+2y=5，若x=-1，则y的值为（　　）
    A．2B．3C．4D．5

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    17．将抛物线y=-$\frac{1}{2}}$x2的图象先向下平移1个单位长度，再向左平移1个单位长度，则平移后的抛物线的解析式为y=-$\frac{1}{2}$（x+1）2-1．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

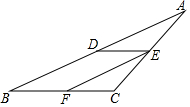    14．如图，已知DE∥BC，EF平分∠CED，∠A=∠CFE，那么EF与AB平行吗？为什么？
    解：因为DE∥BC（已知）
    所以∠DEF=∠CFE（两直线平行，内错角相等）
    因为EF平分∠CED（已知）
    所以∠DEF=∠CFE（角平分线的意义）
    所以∠CFE=∠CEF（等量代换）
    因为∠A=∠CFE（已知）
    所以∠A=∠CEF（等量代换）
    所以EF∥BC（同位角相等，两直线平行）

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    1．一个一元一次不等式组的解集在数轴上表示如图所示，则该不等式组的解集为（　　）
    A．x＜-3B．x≥2C．-3＜x≤2D．无解

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

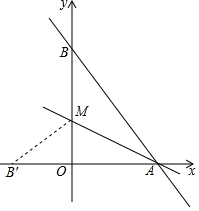    11．直线y=-$\frac{4}{3}$x+8与x轴、y轴分别交于点A和点B，M是OB上的一点，若将△ABM沿AM折叠，点B恰好落在x轴上的点B′处，则M的坐标为（0，3）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

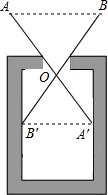    18．如图，将两根等长钢条AA′、BB′的中点O连在一起，使AA′、BB′可以绕着点O自由转动，就做成了一个测量工作，则AB的长等于容器内径A′B′，那么判定△OAB≌△OA′B′的理由是SAS．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

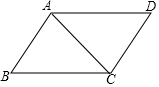    15．如图，在四边形ABCD中，已知AB∥CD，∠B=∠D，在说明∠DAC=∠BCA的解答过程中，填上适当的理由．
    解：∵AB∥CD（已知）
    ∴∠BAC=∠DCA（两直线平行，内错角相等）
    ∠B+∠BCD=180°
    ∠D+∠BAD=180°（两直线平行，同旁内角互补）
    ∵∠B=∠D（已知）
    ∴∠BCD=∠BAD（补角的性质）
    ∵∠DAC=∠BAD-∠BAC
    ∠BCA=∠BCD-∠DCA（已知）
    ∴∠DAC=∠BCA（等量代换）

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    19．甲数为5，乙数为4，则乙数比甲数小20%．

    查看答案和解析>>

    同步练习册答案