Question

如图，已知抛物线的对称轴是x＝4，该抛物线与x轴交于A、B两点，与y轴交于C点．O点是坐标原点，且A、C的坐标分别为(2，0)和(0，3)．

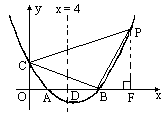
(1)求此抛物线的表达式；

(2)抛物线上有一点P，满足∠PBC＝，求P点的坐标；

(3)y轴上是否存在点E，使得△AOE与以P、B、C为顶点的三角形相似？若存在，求出E点的坐标；若不存在，说明理由．

Answer 1

答案：
解析：

[答案](1)设x＝4与x轴交于D点，则D(4，0)，又A(2，0)，且A，B关于直线x＝4对称．故BD＝AD＝2．从而B(6，0)． 　　设y＝ax2＋bx＋c，则由C(0，3)得c＝3．由A(2，0)，B(6，0)知2和6是方程 　　ax2＋bx＋3＝0的两根．故　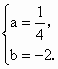　解得 　　故该抛物线的表达式为y＝x2－2x＋3． 　　(2)过P作PF⊥x轴于点F，则∠PBF＝－∠PBC－∠OBC＝－∠OBC＝∠OCB． 　　又∠BOC＝∠PFB，所以△PBF∽△BCO，从而＝． 　　又OB＝6，OC＝3，故PF＝2BF． 　　设BF＝m，则PF＝2m，OF＝6＋m．故点P的坐标为(6＋m，2m)． 　　由点P在抛物线上，得2m＝(6＋m)2－2(6＋m)＋3，即m2－m＝0． 　　解这个方程，得：m1＝0(舍去)，m2＝4．故P(10，8)． 　　(3)存在．E点坐标为(0，)，(0，－)，(0，)和(0，－)． 　　设E点坐标为(0，n)．由已知得BC＝＝3，PB＝＝4． 　　若△AOE∽PBC，则＝，∴＝，n＝±． 　　∴所求E点的坐标为(0，)和(0，－)， 　　若△AOE∽△CBP，则＝，∴＝，n＝±． 　　∴所求E点的坐标为(0，)和(0，－)． 　　[剖析](1)抛物线与x轴两交点关于其对称轴对称，故AD＝BD；(2)先让△PBF∽△BCO，由此得到PF与BF的关系，再用m的代数式表示P点的坐标(由于P点只可能在第一象限，故不需讨论)，然后将P点坐标代入表达式，得到关于m的方程，解方程可求m的值；(3)由于题目未告知两三角形的相似方式，故需分两种情况讨论，又由于E点既可在y轴正半轴上，也可在y轴负半轴上，故OE＝|n|．