Question

14．已知等腰三角形ABC中，AC=BC，AF∥BC，线段CF的垂直平分线DE与AB交于点E，连接EF，EC．
（1）如图1，若∠ACB=90°直接写出∠FEC与∠B之间的数量关系是∠FEC=2∠B．
（2）如图2，若∠ACB＜90°，判断∠FEC与∠B的数量关系，请说明理由．
（3）如图3，在（1）的条件下，延长BA与CF交于点N，若BC=$\sqrt{3}$+3，∠AEF=15°，AF=3-$\sqrt{3}$，求EN的长．

Answer 1

分析 （1）取AB中点M，由△ABC是等腰直角三角形知∠B=∠BCM=45°、∠CME=90°，由DE垂直平分CF知∠FEC=2∠FED=2∠CED、∠EDC=90°，得点C、D、E、M四点共圆即∠CED=∠CMD=45°，故∠FEC=2∠B=90°；
（2）与（1）同理证∠FEC=2∠BCM，根据AC=BC、M是AB中点知∠BCM=90°-∠B，可得；
（3）分别求DM、DF的长，证△NAF～△NMD可求DN的长，在RT△DEN中根据勾股定理可得NE的长．

解答 解（1）如图1，取AB中点M，连接MC、MD、AD．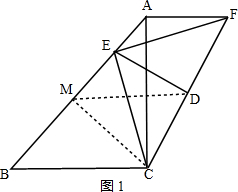

∵AC=BC，∠ACB=90°，AF∥BC，
∴△ABC是等腰直角三角形，四边形ABCF是梯形，
∴CM⊥AB，∠BCM=∠B=45°，
∵DE垂直平分CF，
∴∠CED=∠FED，DM是梯形ABCF的中位线，
∴DM∥BC∥AF，
∴∠CMD=∠BCM=∠45°，
∵DE⊥CF，
∴∠CME=∠CDE=90°，
∴点C、D、E、M四点共圆，
∴∠FDE=∠CED=∠CMD=45°，
∴∠FEC=2∠CED=90°=2∠B；
（2）∠CEF=180°-2∠B，
如图2，取AB中点M，连接CM、DM，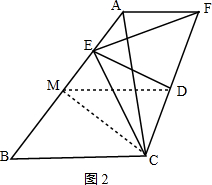

与（1）同理，∠FED=∠CED=∠CMD=∠BCM，
∴∠FEC=2∠BCM，
又∵AC=BC，M是AB中点，
∴CM⊥AB，
∴∠BCM=90°-∠B，
∴∠FEC=2（90°-∠B）=180°-2∠B；
（3）如图3，取AB中点M，连接CM、DM，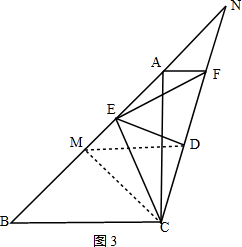

由（1）知，DM是梯形ABCF的中位线，且AC=BC=$3+\sqrt{3}$，AF=$3-\sqrt{3}$，
∴DM=$\frac{1}{2}$（AF+BC）=3，
∵∠CEF=2∠B=90°，DE垂直平分CF，
∴CF=$\sqrt{A{C}^{2}+A{F}^{2}}$=2$\sqrt{6}$，
∴DE=DF=$\frac{1}{2}$CF=$\sqrt{6}$，
又∵AF∥MD，
∴△NAF～△NMD，
∴$\frac{NF}{ND}=\frac{DN-DF}{DN}=\frac{AF}{MD}$，即$\frac{DN-\sqrt{6}}{DN}=\frac{3-\sqrt{3}}{3}$，
解得：DN=3$\sqrt{2}$，
在RT△DEN中，EN=$\sqrt{D{N}^{2}+D{E}^{2}}$=2$\sqrt{6}$．
故答案为：∠FEC=2∠B．

点评 本题主要考查梯形中位线定理、等腰三角形性质、中垂线性质等，作底边上中线将待求角与已知角联系到一起是关键．