
【题目】反比例函数y= ![]() 的图象经过点A(﹣1,2),则当x>1时,函数值y的取值范围是( )
的图象经过点A(﹣1,2),则当x>1时,函数值y的取值范围是( )
A.y>﹣1
B.﹣1<y<0
C.y<﹣2
D.﹣2<y<0
【答案】D
【解析】解:根据题意, ![]() =2,
=2,
解得k=﹣2,
∴反比例函数解析式为y=﹣ ![]() ,
,
在第四象限内,y值随x的增大而增大,
∴y>﹣ ![]() ,即y>﹣2,
,即y>﹣2,
又∵函数图象在第四象限内,
∴y<0,
∴函数值y的取值范围是﹣2<y<0.
所以答案是:D.
【考点精析】解答此题的关键在于理解一元一次不等式的解法的相关知识,掌握步骤:①去分母;②去括号;③移项;④合并同类项; ⑤系数化为1(特别要注意不等号方向改变的问题),以及对反比例函数的性质的理解,了解性质:当k>0时双曲线的两支分别位于第一、第三象限,在每个象限内y值随x值的增大而减小; 当k<0时双曲线的两支分别位于第二、第四象限,在每个象限内y值随x值的增大而增大.


 期末100分闯关海淀考王系列答案
期末100分闯关海淀考王系列答案科目:初中数学 来源: 题型:
【题目】已知,点O是直线AB上一点,OC、OD为从点O引出的两条射线,∠BOD=30°,∠COD=![]() ∠AOC.
∠AOC.
(1)如图①,求∠AOC的度数;
(2)如图②,在∠AOD的内部作∠MON=90°,请直接写出∠AON与∠COM之间的数量关系 ;
(3)在(2)的条件下,若OM为∠BOC的角平分线,试说明∠AON=∠CON.

查看答案和解析>>
科目:初中数学 来源: 题型:
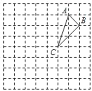
【题目】已知:如图,在边长为1的小正方形网格中,△ABC的顶点都在格点上,建立适当的平面直角坐标系xOy,使得点A、B的坐标分别为(2,3)、(3,2).
(1)在网格中画出满足要求的平面直角坐标系,写出点C的坐标为 ;
(2)若点P是x轴上的一个动点,则PA+PB的最小值为 .(直接写出结果)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABP中,C是BP边上一点,∠PAC=∠PBA,⊙O是△ABC的外接圆,AD是⊙O的直径,且交BP于点E. 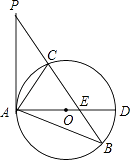
(1)求证:PA是⊙O的切线;
(2)过点C作CF⊥AD,垂足为点F,延长CF交AB于点C,若ACAB=12,求AC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
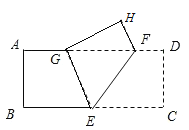
【题目】如图,把长方形纸片ABCD沿EF折叠后,使得点D落在点H的位置上,点C恰好落在边AD上的点G处,连接EG.
(1)△GEF是等腰三角形吗?请说明理由;
(2)若CD=4,GD=8,求HF的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是某商品的标志图案,AC与BD是⊙O的两条直径,首尾顺次连接点A,B,C,D,得到四边形ABCD.若AC=10cm,∠BAC=36°,则图中阴影部分的面积为( ) 
A.5πcm2
B.10πcm2
C.15πcm2
D.20πcm2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知点A、B、C是数轴上三点,O为原点.点C对应的数为6,BC=4,AB=12.
(1)求点A、B对应的数;
(2)动点P、Q分别同时从A、C出发,分别以每秒6个单位和3个单位的速度沿数轴正方向运动.M为AP的中点,N在CQ上,且CN=![]() CQ,设运动时间为t(t>0).
CQ,设运动时间为t(t>0).
①求点M、N对应的数(用含t的式子表示); ②t为何值时,OM=2BN.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD的面积为12,△ABC是等边三角形,点E在正方形ABCD内,对角线AC上有一点P使PE+PD的和最小,这个最小值为( )

A. ![]() B.
B. ![]() C. 3 D.
C. 3 D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,火车站、码头分别位于A,B两点,直线a和b分别表示铁路与河流.

(1)从火车站到码头怎样走最近,画图并说明理由;
(2)从码头到铁路怎样走最近,画图并说明理由;
(3)从火车站到河流怎样走最近,画图并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com