
【题目】如图,抛物线交![]() 轴于
轴于![]() 、
、![]() 两点(点
两点(点![]() 在点
在点![]() 的左边),交
的左边),交![]() 轴于点
轴于点![]() ,直线
,直线![]() 经过点
经过点![]() 与
与![]() 轴交于点
轴交于点![]() ,抛物线的顶点坐标为
,抛物线的顶点坐标为![]() .
.
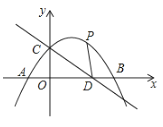
(1)请你求出![]() 的长及抛物线的函数关系式;
的长及抛物线的函数关系式;
(2)求点![]() 到直线
到直线![]() 的距离;
的距离;
(3)若点![]() 是抛物线位于第一象限部分上的一个动点,则当点
是抛物线位于第一象限部分上的一个动点,则当点![]() 运动至何处时,恰好使
运动至何处时,恰好使![]() ,请你直接写出此时的
,请你直接写出此时的![]() 点坐标.
点坐标.
【答案】(1)5,![]() 或
或![]() ;(2)
;(2)![]() ;(3)P
;(3)P![]() .
.
【解析】
(1)求出点C,D的坐标,再用勾股定理求得CD的长;设抛物线为y=a(x-2)2+4,将点C坐标代入求得a,即可得出抛物线的函数表达式;
(2)过点B直线CD的垂线,垂足为H,在Rt△BDH中,利用锐角三角函数即可求得点B到直线CD的距离;
(3)构造等腰直角△EDC和K字型全等图形可得E点坐标,继而可求直线ED的解析式,而直线ED与抛物线的交点即为所求的点P.
解:(1)∵![]() ,
,
∴C(0,3),D(4,0),
∵∠COD=90°,
∴CD=![]() =5.
=5.
设抛物线为y=a(x﹣2)2+4,将点C(0,3)代入抛物线,
得3=4a+4,
∴![]() ,
,
∴抛物线的函数关系式为![]() 或
或![]() ;
;
(2)解:过点B作BH⊥CD于H,

由![]() ,
,
可得x1=﹣2,x2=6,
∴点B的坐标为(6,0),
∵OC=3,OD=4,CD=5,
∴BD=OB﹣OD=6﹣4=2,
在Rt△DHB中,
∵BH=BDsin∠BDH=BDsin∠CDO=2×![]() =
=![]() ,
,
∴点B到直线CD的距离为![]() .
.
(3作∠CDP=45°交抛物线于点P,作EC⊥CD交射线DP于点E,作EF⊥y轴于F
∴∠CED=∠CDP=45°, ∴CE=CD
∵∠ECF+∠OCD=90°,∠ECF +∠FEC=90°
∴∠OCD=∠FEC
∵ ∠CFE=∠DOC=90°,
∴△
∴ CF=OD=4,EF=OC=3, OF=OC+CF=7
∴点E(3,7),
由E(3,7),D(4,0),可得直线ED的解析式为:y=﹣7x+28,
解方程组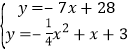 ,
,
得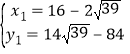 ,
, 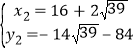 (不合题意,舍去);
(不合题意,舍去);
所以,此时P点坐标为(![]() ,
,![]() ).
).


 状元坊全程突破导练测系列答案
状元坊全程突破导练测系列答案 直通贵州名校周测月考直通名校系列答案
直通贵州名校周测月考直通名校系列答案科目:初中数学 来源: 题型:
【题目】苏科版九年级下册数学课本91页有这样一道习题:


(1)复习时,小明与小亮、数学老师交流了自己的两个见解,并得到了老师的认可:
①可以假定正方形的边长AB=4a,则AE=DE=2a,DF=a,利用“两边分别成比例且夹角相等的两个三角形相似”可以证明△ABE∽△DEF;请结合提示写出证明过程.
②图中的相似三角形共三对,而且可以借助于△ABE与△DEF中的比例线段来证明△EBF与它们相似.证明过程如下:

(2)交流之后,小亮尝试对问题进行了变化,在老师的帮助下,提出了新的问题,请你解答:
已知:如图,在矩形ABCD中,E为AD的中点,EF⊥EC交AB于F,连结FC.
(AB>AE)

①求证:△AEF∽△ECF;
②设BC=2,AB=a,是否存在a值,使得△AEF与△BFC相似.若存在,请求出a的值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
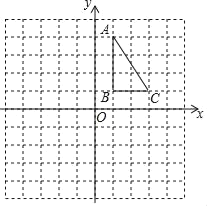
【题目】如图,正方形网格中,每个小正方形的边长都是一个单位长度,在平面直角坐标系内,△ABC的三个顶点坐标分别为A(1,4),B(1,1),C(3,1).
(1)画出△ABC左平移4个单位得到的△A1B1C1,且A1的坐标为 ;
(2)画出△ABC绕点O顺时针旋转90°后的△A2B2C2;
(3)在(2)的条件下,求线段BC扫过的面积(结果保留π).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2017年9月,我国中小学生迎来了新版“教育部统编义务教育语文教科书”,本次“统编本”教材最引人关注的变化之一是强调对传统文化经典著作的阅读,某校对A《三国演义》、B《红楼梦》、C《西游记》、D《水浒》四大名著开展“最受欢迎的传统文化经典著作”调查,随机调查了若干名学生(每名学生必选且只能选这四大名著中的一部)并将得到的信息绘制了下面两幅不完整的统计图:

(1)本次一共调查了 名学生;
(2)请将条形统计图补充完整;
(3)某班语文老师想从这四大名著中随机选取两部作为学生暑期必读书籍,请用树状图或列表的方法求恰好选中《三国演义》和《红楼梦》的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学为推动“时刻听党话 永远跟党走”校园主题教育活动,计划开展四项活动:A:党史演讲比赛,B:党史手抄报比赛,C:党史知识竞赛,D:红色歌咏比赛.校团委对学生最喜欢的一项活动进行调查,随机抽取了部分学生,并将调查结果绘制成图1,图2两幅不完整的统计图.请结合图中信息解答下列问题:
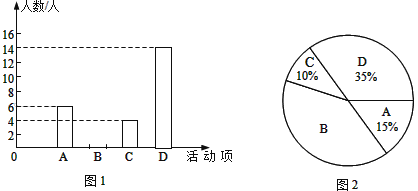
(1)本次共调查了 名学生;
(2)将图1的统计图补充完整;
(3)已知在被调查的最喜欢“党史知识竞赛”项目的4个学生中只有1名女生,现从这4名学生中任意抽取2名学生参加该项目比赛,请用画树状图或列表的方法,求出恰好抽到一名男生一名女生的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在一笔直的海岸线上有A、B两个码头,A在B的正东方向,一艘小船从A码头沿北偏西60°的方向行驶了30海里到达点P处,此时从B码头测得小船在北偏东45°的方向.求此时小船到B码头的距离(即BP的长)和A、B两个码头间的距离(结果都保留根号).
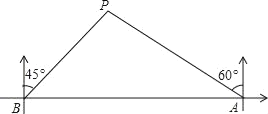
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某五金商店准备从机械厂购进甲、乙两种零件进行销售.若每个甲种零件的进价比每个乙种零件的进价少2元,且用900元正好可以购进50个甲种零件和50个乙种零件.
(1)求每个甲种零件、每个乙种零件的进价分别为多少元?
(2)若该五金商店本次购进甲种零件的数量比购进乙种零件的数量的3倍还少5个,购进两种零件的总数量不超过95个,该五金商店每个甲种零件的销售价格为12元,每个乙种零件的销售价格为15元,则将本次购进的甲、乙两种零件全部售出后,可使销售两种零件的总利润(利润=售价-进价)超过371元,通过计算求出该五金商店本次从机械厂购进甲、乙两种零件有哪几种方案?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com