
����Ŀ����ʮһ���ƽ����ڼ䣬С��Ҫ�븸ĸ������棬����2�����º�3������(���·��Ϳ��ӷֱ�װ������������)��������ɫ�к�ɫ����ɫ�������к�ɫ����ɫ����ɫ��
������
��1��С�������ó�һ�����Ӻ�һ���������һ�ף���(����״ͼ���б���)�е�һ���г����п��ܳ��ֽ����
��2�����һ���·���С�������õ���ɫ����ĸ����Ƕ��٣�
��3���������ó�һ�����º�һ�����㴩�ϵ���ɫ������ͬ�ĸ����Ƕ��٣�
���𰸡�
��1��
�⣺�б����ϣ�
���� | ��ɫ | ��ɫ | ��ɫ |
��ɫ | ��ɫ����ɫ | ��ɫ����ɫ | ��ɫ����ɫ |
��ɫ | ��ɫ����ɫ | ��ɫ����ɫ | ��ɫ����ɫ |
����С�������ó�һ�����Ӻ�һ���������һ�ף����п��ܳ��ֵĽ����6�֣�
��2��
��ɫ����������֣����Ը����� ![]() ��
��
��3��
��ɫ��ͬ��ռ���֣����Ը����� ![]() ��
��
����������Ϊ������Ҫ������ɣ����Բ����б������߲�����״ͼ�����Ƚϼ�����ʱҪע���ǷŻ�ʵ�黹�Dz��Ż�ʵ�飮�������ڷŻ�ʵ�飮���ݱ���ɵ�����������ҵ���ɫ����ռȫ������Ķ��٣���ɫ��ͬ�����ռȫ������Ķ��٣�
�����㾫�������ڱ��⿼����б�������״ͼ������Ҫ�˽һ������Ҫ�����������������ʱ�����б����Ͳ������ˣ�Ϊ�˲��ز�©���г����п��ܵĽ����ͨ��������״ͼ������ʲ��ܵó���ȷ�𰸣�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
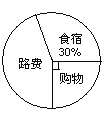
����Ŀ��Τκһ��������������֧��կ�����Σ�Τκ����;����֧������Ƴ������µ�ͳ��ͼ�������ǹ����������8600Ԫ��
����һ���ֵķ���ռ����֧����![]() �������˶���Ԫ��
�������˶���Ԫ��
����ʳ���ϻ����˶���Ԫ?
����һ��������·��ռ��֧���İٷ�֮���������˶���Ԫ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����㣺
��1��![]() +����
+����![]() ��+
��+![]() +����
+����![]() ����
����
��2����![]() ��
��![]() +
+![]() ���£���
���£���![]() ����
����
��3����15+����2��3��8������3����![]() ��
��
��4����13������5��2��![]() +
+![]() .
.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ1����OΪֱ��AB��һ��������O������OC��ʹ��BOC=120������һֱ�����ǰ��ֱ�Ƕ�����ڵ�O����һ��OM������OB������һ��ON��ֱ��AB���·���

��1����ͼ1�е����ǰ��Ƶ�O��ʱ����ת��ͼ2��ʹһ��OM����BOC���ڲ�����ǡ��ƽ����BOC��������ʱֱ��ON�Ƿ�ƽ����AOC����˵��������
��2����ͼ1�е����ǰ��Ƶ�O��ÿ��10�����ٶ���˳ʱ�뷽����תһ��������ת�Ĺ���������t��ʱ��ֱ��ONǡ��ƽ�������AOC���� t��ֵΪ �루ֱ��д���������
��3����ͼ1�е����ǰ��Ƶ�O˳ʱ����ת��ͼ3��ʹON����AOC���ڲ�����̽��������ת����������AOM����NOC�IJ��Ƿ����仯��������������������ֵ�����仯���������ı仯��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
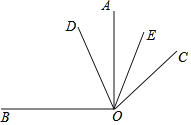
����Ŀ����ͼ����֪��ͬһƽ����OA��OB��OC��OA�Ƶ�O˳ʱ�뷽����ת��������90�����ȵõ���ODƽ����BOC��OEƽ����AOC��
��1������=60����AOC=60��ʱ������BOC����DOE��
��2�������ı仯�����У���DOE�Ķ�����һ����ֵ�����Ƕ�ֵ����������ֵ�������Ƕ�ֵ����˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
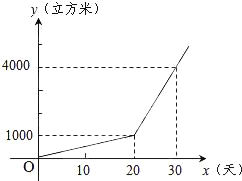
����Ŀ��ijũ����ֲһ�־����������ˮ��y����3������ֲʱ��x���죩֮��ĺ�����ϵʽ��ͼ��ʾ��
��1����20�������ˮ��Ϊ������3��
��2����x��20ʱ����y��x֮��ĺ�����ϵʽ��
��3����ֲʱ��Ϊ������ʱ������ˮ���ﵽ7000��3��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����һ�������Ĵ�����װ��3����������ɰ������dz���ɫ�ⶼ��ͬ���ڲ���������������ǰ���£�С��Ϊ�������а��������������°취�������������һ������ɫ��Żش��У����ҡ�Ⱥ����������һ������ɫ���������ظ��������̣�С������100�Σ�����20�������������������ݣ�С�����ƿڴ��а����Լ��()
A.10��
B.12 ��
C.15 ��
D.18��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ͬѧ�ǣ������������ϵ�һ���˶������Ȱ������˶�����֪����������У�ʤһ����3�֣�ƽһ����1�֣���һ����0�֣�һ�ӹ�����30������������9��������47�֣���ô�����ʤ�ˣ�������
A. 10�� B. 11�� C. 12�� D. 13��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ƽ��ֱ������ϵxOy�У���O�İ뾶Ϊ1��P������ϵ������һ�㣬��P����O�ľ���SP�Ķ������£�����P��Բ��O�غϣ���SPΪ��O�İ뾶��������P��Բ��O���غϣ�������OP����O�ڵ�A����SPΪ�߶�AP�ij��ȣ� ͼ1Ϊ��P�ڡ�O�������ʾ��ͼ��
��1������B��1��0����C��1��1���� ![]() ����SB=��SC=��SD=��
����SB=��SC=��SD=��
��2����ֱ��y=x+b�ϴ��ڵ�M��ʹ��SM=2����b��ȡֵ��Χ��
��3����֪��P��Q��x���ϣ�RΪ�߶�PQ������һ�㣮���߶�PQ�ϴ���һ��T������T�ڡ�O����ST��SR �� ֱ��д�������������߶�PQ���ȵ����ֵ��
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com