
【题目】如图,△APB中,AB=2,∠APB=90°,在AB的同侧作正△ABD、正△APE和正△BPC,则四边形PCDE面积的最大值是__.
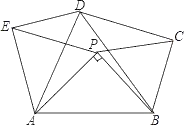
【答案】1.
【解析】试题分析:先延长EP交BC于点F,得出PF⊥BC,再判定四边形CDEP为平行四边形,根据平行四边形的性质得出:四边形CDEP的面积=EP×CF=a×![]() b=
b=![]() ab,最后根据
ab,最后根据![]() ,判断
,判断![]() ab的最大值即可.
ab的最大值即可.
试题解析:延长EP交BC于点F,∵∠APB=90°,∠AOE=∠BPC=60°,∴∠EPC=150°,∴∠CPF=180°﹣150°=30°,∴PF平分∠BPC,又∵PB=PC,∴PF⊥BC,设Rt△ABP中,AP=a,BP=b,则
CF=![]() CP=
CP=![]() b,
b,![]() ,∵△APE和△ABD都是等边三角形,∴AE=AP,AD=AB,∠EAP=∠DAB=60°,∴∠EAD=∠PAB,∴△EAD≌△PAB(SAS),∴ED=PB=CP,同理可得:△APB≌△DCB(SAS),∴EP=AP=CP,∴四边形CDEP是平行四边形,∴四边形CDEP的面积=EP×CF=a×
,∵△APE和△ABD都是等边三角形,∴AE=AP,AD=AB,∠EAP=∠DAB=60°,∴∠EAD=∠PAB,∴△EAD≌△PAB(SAS),∴ED=PB=CP,同理可得:△APB≌△DCB(SAS),∴EP=AP=CP,∴四边形CDEP是平行四边形,∴四边形CDEP的面积=EP×CF=a×![]() b=
b=![]() ab,又∵
ab,又∵![]() ≥0,∴2ab≤
≥0,∴2ab≤![]() ,∴
,∴![]() ab≤1,即四边形PCDE面积的最大值为1.故答案为:1.
ab≤1,即四边形PCDE面积的最大值为1.故答案为:1.


 金博士一点全通系列答案
金博士一点全通系列答案科目:初中数学 来源: 题型:
【题目】平面直角坐标系 xOy 中,定义:已知图形 W 和直线 l.如果图形 W 上存在一点 Q,使得点 Q 到直线 l 的距离小于或等于 k,则称图形 W 与直线 l“k 关联”,设图形 W:线段 AB,其中点 A(t,0)、点 B(t+2, 0).
(1)线段AB的长是 ;
(2)当t=1 时,
①已知直线y=﹣x﹣1,点A到该直线的距离为 ;
②已知直线y=﹣x+b,若线段AB与该直线“![]() 关联”,求b的取值范围。
关联”,求b的取值范围。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了迎接旅发大会顺利在织金召开,织金某巡警骑摩托车在南北大道上巡逻,一天他从岗亭出发,晚上停留在A处,规定向北方向为正,当天行驶情况记录如下(单位:千米):+10,﹣8,+7,﹣15,+6,﹣16,+4,﹣4
(1)A处在岗亭何方?距离岗亭多远?
(2)若摩托车每行驶1千米耗油0.5升,这一天共耗油多少升?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算下列各题:
(1)1-4+3-0.5
(2)(![]() )×6
)×6
(3)40×(-5)-(-3)÷![]()
(4)-14+![]() -2×(-2)2
-2×(-2)2
(5)32-(-![]() )×
)×![]() +(-8)÷
+(-8)÷![]()
(6)(-![]() )3+
)3+![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校计划购买若干台电脑,现从两家商场了解到同一型号电脑每台报价均为4000元,并且多买都有一定的优惠.甲商场的优惠条件是:第一台按原价收费,其余每台优惠25%;乙商场的优惠条件是:每台优惠20%.
(1)设该学校所买的电脑台数是x台,选择甲商场时,所需费用为![]() 元,选择乙商场时,所需费用为
元,选择乙商场时,所需费用为![]() 元,请分别写出
元,请分别写出![]() ,
, ![]() 与x之间的关系式;
与x之间的关系式;
(2)该学校如何根据所买电脑的台数选择到哪间商场购买,所需费用较少?
查看答案和解析>>
科目:初中数学 来源: 题型:
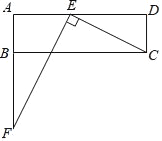
【题目】如图,在矩形ABCD中,已知 AD>AB.在边AD上取点E,连结CE.过点E作EF⊥CE,与边AB的延长线交于点F.
(1)证明:△AEF∽△DCE.
(2)若AB=4,AE=6,AD=14,求线段AF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是 2019 年五月的月历,“T”型、“田”型两个阴影图形分别覆盖其中四个方格(可以重叠覆盖),设“T”型阴影覆盖的最小数字为 a,四个数字之和为 S1,“田”型阴影覆盖的最小数字为 b,四个数字之和为 S2.
(1) S1 的值能否为 50?若能,求 a 的值;若不能,说明理由;
(2)S1+ S2 值能否为 35,若能,求 a,b 的值;若不能,说明理由;
(3)若 S1+ S2=43,求 S1-S2 的值为 (直接写结果).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某片果园有果树80棵,现准备多种一些果树提高果园产量,但是如果多种树,那么树之间的距离和每棵树所受光照就会减少,单棵树的产量随之降低,若该果园每棵果树产果y千克,增种果树x棵,它们之间的函数关系如图所示.

(1)求y与x之间的函数解析式;
(2)在投入成本最低的情况下,增种果树多少棵时,果园可以收获果实6750千克?
(3)当增种果树多少棵时,果园的总产量w(千克)最大?最大产量是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com