
【题目】如图,点O为线段AD上一点,CO⊥AD于点O,OA=OB,OC=OD,点M、N分别是AC、BD的中点,连接OM、ON、MN.
(1)求证:AC=BD;
(2)试判断△MON的形状,并说明理由;
(3)若AC=2,在图2中,点M在DB的延长线上,求△AMD的面积.

【答案】(1)见解析(2)等腰直角三角形(3)![]()
【解析】
(1)根据已知条件可以得出△AOC≌△BOD就可以得出AC=BD,
(2)由直角三角形的性质就可以得出MO=NO=![]() AC=
AC=![]() BD,从而得出∠A=∠AOM,∠NBO=∠NOB,又因为△AOC≌△BOD所以∠A=∠OBD,从而得出∠NOB=∠MOA,就可以得出∠NOM=90°,得出△MON的形状。
BD,从而得出∠A=∠AOM,∠NBO=∠NOB,又因为△AOC≌△BOD所以∠A=∠OBD,从而得出∠NOB=∠MOA,就可以得出∠NOM=90°,得出△MON的形状。
(3)根据AC=2得出MO= NO=1,AM=DN=1,根据勾股定理可得MN=![]() ,所以DM=
,所以DM=![]() +1
+1
由△AOC≌△BOD得出∠C=∠D,由∠C+∠A=90![]() 可得∠D+∠A=90
可得∠D+∠A=90![]() ,所以∠AMD=90
,所以∠AMD=90![]() ,根据三角形的面积公式即可解答。
,根据三角形的面积公式即可解答。
证明:∵CO⊥AD
∴![]() =90
=90![]()
在△AOC和△BOD中,
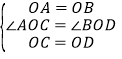 ,
,
∴△AOC≌△BOD(SAS),
∴AC=BD,
(2) ∵M、N分别是AC、BD的中点,∠AOC=∠BOD=90°,
∴MO=MA=![]() AC,NO=NB=
AC,NO=NB=![]() BD,
BD,
∵AC=BD,
∴MO=MA= NO=NB
∴∠A=∠AOM,∠NBO=∠NOB,
∵△AOC≌△BOD
∴∠A=∠OBN,
∴∠AOM=∠BON.
∵∠AOM+∠COM=90°,
∴∠BON+∠COM=90°,
∴∠MON=90°.
∴△MON是等腰直角三角形.
(3)∵AC=2
由(2)可得MO= NO=1,AM=DN=1
根据勾股定理可得MN=![]() ,
,
∴DM=![]() +1
+1
∵△AOC≌△BOD
∴∠C=∠D
∵![]() =90
=90![]()
∴∠C+∠A=90![]()
∴∠D+∠A=90![]() ∴∠AMD=90
∴∠AMD=90![]() ,
,
∴![]() MA.DM=
MA.DM=![]() +1)=
+1)=![]()


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】如图,将矩形ABCD沿对角线AC翻折,点B落在点F处,FC交AD于E.
(1)求证:△AFE≌△CDF;
(2)若AB=4,BC=8,求图中阴影部分的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数y=kx+b(k≠0)的图象与x轴的交点坐标为(-2,0),则下列说法:①y随x的增大而减小;②关于x的方程kx+b=0的解为x=-2;③kx+b>0的解集是x>-2;④b<0.其中正确的有__________.(填序号)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线 ![]() 与
与 ![]() 轴交于点
轴交于点 ![]() (点
(点 ![]() 分别在
分别在 ![]() 轴的左右两侧)两点,与
轴的左右两侧)两点,与 ![]() 轴的正半轴交于点
轴的正半轴交于点 ![]() ,顶点为
,顶点为 ![]() ,已知点
,已知点 ![]() .
.
(1)求点 ![]() 的坐标;
的坐标;
(2)判断△ ![]() 的形状,并说明理由;
的形状,并说明理由;
(3)将△ ![]() 沿
沿 ![]() 轴向右平移
轴向右平移 ![]() 个单位(
个单位( ![]() )得到△
)得到△ ![]() .△
.△ ![]() 与△
与△ ![]() 重叠部分(如图中阴影)面积为
重叠部分(如图中阴影)面积为 ![]() ,求
,求 ![]() 与
与 ![]() 的函数关系式,并写出自变量
的函数关系式,并写出自变量 ![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】你能求(x﹣1)(x99+x98+x97+…+x+1)的值吗?遇到这样的问题,我们可以先思考一下,从简单的情形入手.先分别计算下列各式的值.
①(x﹣1)(x+1)=x2﹣1
②(x﹣1)(x2+x+1)=x3﹣1
③(x﹣1)(x3+x2+x+1)=x4﹣1
……
由此我们可以得到:(x﹣1)(x99+x98+x97+…+x+1)=
请你利用上面的结论,再完成下面两题的计算:
(1)(﹣2)50+(﹣2)49+(﹣2)48+…+(﹣2)+1
(2)若x3+x2+x+1=0,求x2019的值
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,直线l1:![]() 与坐标轴交于A,B两点,直线l2:
与坐标轴交于A,B两点,直线l2:![]() (
(![]() ≠0)与坐标轴交于点C,D.
≠0)与坐标轴交于点C,D.
(1)求点A,B的坐标;
(2)如图,当![]() =2时,直线l1,l2与相交于点E,求两条直线与
=2时,直线l1,l2与相交于点E,求两条直线与![]() 轴围成的△BDE的面积;
轴围成的△BDE的面积;
(3)若直线l1,l2与![]() 轴不能围成三角形,点P(a,b)在直线l2:
轴不能围成三角形,点P(a,b)在直线l2:![]() (k≠0)上,且点P在第一象限.
(k≠0)上,且点P在第一象限.
①求![]() 的值;
的值;
②若![]() ,,求
,,求![]() 的取值范围.
的取值范围.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图:E在△ABC的AC边的延长线上,D点在AB边上,DE交BC于点F,DF=EF,BD=CE.求证:△ABC是等腰三角形.(过D作DG∥AC交BC于G)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图:为了测量某棵树的高度,小刚用长为2m的竹竿做测量工具,移动竹竿,使竹竿、树的顶端的影子恰好落在地面的同一点,此时,竹竿与这一点距离6m,与树相距15m,那么这棵的高度为( )
A.5米
B.7米
C.7.5米
D.21米
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下面是某同学对多项式(x2-4x+2)(x2-4x+6)+4进行因式分解的过程.
解:设x2-4x=y
原式=(y+2)(y+6)+4 (第一步)
=y2+8y+16 (第二步)
=(y+4)2(第三步)
=(x2-4x+4)2(第四步)
回答下列问题:
(1)该同学第二步到第三步运用了因式分解的_______.
A.提取公因式 |
B.平方差公式 |
C.两数和的完全平方公式 |
D.两数差的完全平方公式 |
(2)该同学因式分解的结果是否彻底?________.(填“彻底”或“不彻底”)若不彻底,请直接写出因式分解的最后结果_________ .
(3)请你模仿以上方法尝试对多项式(x2-2x)(x2-2x+2)+1进行因式分解.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com