
【题目】如图,直线l过正方形ABCD的顶点A,BE⊥l于点E,DF⊥l于点F,若BE=2,DF=4,则EF的长为( ) 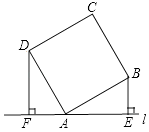
A.2 ![]()
B.2 ![]()
C.6
D.8
【答案】C
【解析】解:∵正方形ABCD,
∴AD=AB,∠DAB=90°,
∵BE⊥l于点E,DF⊥l于点F,
∴∠AFD=∠AEB=90°,
∴∠FAD+∠FDA=90°,且∠EAB+∠FAD=90°,
∴∠FDA=∠EAB,
在△ABE和△ADF中
∵ 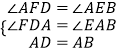 ,
,
∴△ABE≌△DAF(AAS),
即AE=DF=2,AF=BE=4,
∴EF=AE+AF=4+2=6,
故选C.
【考点精析】认真审题,首先需要了解正方形的性质(正方形四个角都是直角,四条边都相等;正方形的两条对角线相等,并且互相垂直平分,每条对角线平分一组对角;正方形的一条对角线把正方形分成两个全等的等腰直角三角形;正方形的对角线与边的夹角是45o;正方形的两条对角线把这个正方形分成四个全等的等腰直角三角形).


 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案科目:初中数学 来源: 题型:
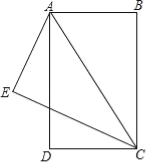
【题目】如图,已知BA=AE=DC,AD=EC,CE⊥AE,垂足为E.
(1)求证:△DCA≌△EAC;
(2)只需添加一个条件,即 ,可使四边形ABCD为矩形.请加以证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学七、八年级各选派10名选手参加学校举办的知识竞赛,竞赛计分采用10分制,选手得分均为整数,成绩达到6分或6分以上为合格,达到9分或10分为优秀.七、八年级两支代表队选手成绩分布的条形统计图和成绩统计分析表如下所示.
队别 | 平均分 | 众数 | 中位数 | 方差 | 合格率 | 优秀率 |
七年级 | 6.7 | a | m | 3.41 | 90% | 20% |
八年级 | 7.1 | p | q | 1.69 | 80% | 10% |
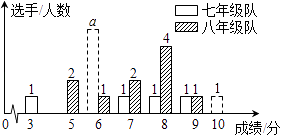
(1)请依据图表中的数据,求出a的值;并直接写出表格中m,p,q的值;
(2)有人说七年级的合格率、优秀率均高于八年级,所以七年级队成绩比八年级队好,但也有人说八年级队成绩比七年级队好.请你给出两条支持八年级队成绩好的理由、
查看答案和解析>>
科目:初中数学 来源: 题型:
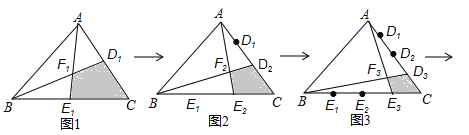
【题目】设△ABC的面积为1.
如图1,分别将AC,BC边2等分,D1,E1是其分点,连接AE1,BD1交于点F1,得到四边形CD1F1E1,其面积S1=![]() .
.
如图2,分别将AC,BC边3等分,D1,D2,E1,E2是其分点,连接AE2,BD2交于点F2,得到四边形CD2F2E2,其面积S2=![]() ;
;
如图3,分别将AC,BC边4等分,D1,D2,D3,E1,E2,E3是其分点,连接AE3,BD3交于点F3,得到四边形CD3F3E3,其面积S3=![]() ;
;
…
按照这个规律进行下去,若分别将AC,BC边(n+1)等分,…,得到四边形CDnEnFn,其面积S= .
查看答案和解析>>
科目:初中数学 来源: 题型:
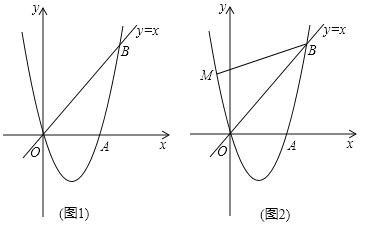
【题目】如图1,经过原点O的抛物线![]() (a≠0)与x轴交于另一点A(
(a≠0)与x轴交于另一点A(![]() ,0),在第一象限内与直线y=x交于点B(2,t).
,0),在第一象限内与直线y=x交于点B(2,t).
(1)求这条抛物线的表达式;
(2)在第四象限内的抛物线上有一点C,满足以B,O,C为顶点的三角形的面积为2,求点C的坐标;
(3)如图2,若点M在这条抛物线上,且∠MBO=∠ABO,在(2)的条件下,是否存在点P,使得△POC∽△MOB?若存在,求出点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法不正确的是( )
A. 等腰三角形是轴对称图形
B. 三角相等的三角形是等边三角形
C. 如果两个三角形成轴对称,那么这两个三角形一定全等
D. 若A,B两点关于直线MN对称,则AB垂直平分MN
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com