
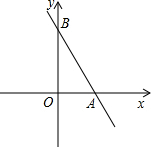
 直线y=-$\frac{4}{3}$x+4与x轴、y轴分别交于点A、B,M是y轴上一点,若将△ABM沿AM折叠,点B恰好落在x轴上,则点M的坐标为(0,$\frac{3}{2}$)或(0,-6).
直线y=-$\frac{4}{3}$x+4与x轴、y轴分别交于点A、B,M是y轴上一点,若将△ABM沿AM折叠,点B恰好落在x轴上,则点M的坐标为(0,$\frac{3}{2}$)或(0,-6). 分析 设沿直线AM将△ABM折叠,点B正好落在x轴上的C点,则有AB=AC,而AB的长度根据已知可以求出,所以C点的坐标由此求出;又由于折叠得到CM=BM,在直角△CMO中根据勾股定理可以求出OM,也就求出M的坐标.
解答  解:如右图所示,设沿直线AM将△ABM折叠,点B正好落在x轴上的C点,A(3,0),B(0,4),
解:如右图所示,设沿直线AM将△ABM折叠,点B正好落在x轴上的C点,A(3,0),B(0,4),
则有AB=AC,
又OA=3,OB=4,
∴AB=5,
故求得点C的坐标为:(-2,0).
再设M点坐标为(0,b),
则CM=BM=4-b,
∵CM2=CO2+OM2,
∴b=$\frac{3}{2}$,
∴M(0,$\frac{3}{2}$),
此外当AM为角BAO的外角平分线时,同理求得一M点(0,-6)
故答案为:(0,$\frac{3}{2}$)或(0,-6).
点评 本题综合考查了翻折变换,题中利用折叠知识与直线的关系以及直角三角形等知识求出线段的长是解题的关键


科目:初中数学 来源: 题型:填空题
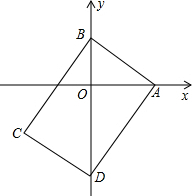 如图,在矩形ABCD中,AB=3,AD=4,顶点A、B、D在坐标轴上.将矩形ABCD平移,使点C与原点O重合,则平移后点A的对应点A′的坐标为(4.8,1.4).
如图,在矩形ABCD中,AB=3,AD=4,顶点A、B、D在坐标轴上.将矩形ABCD平移,使点C与原点O重合,则平移后点A的对应点A′的坐标为(4.8,1.4).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
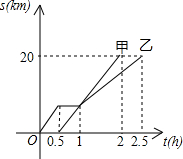 甲乙两同学在假日期间,义务担任“城市文明宣传员”.两人都从A地出发,骑自行车沿同一条路线宣传,均行驶到B地.他们离出发地距离S(km)与行驶时间t(h)之间的函数关系的图象如图所示.
甲乙两同学在假日期间,义务担任“城市文明宣传员”.两人都从A地出发,骑自行车沿同一条路线宣传,均行驶到B地.他们离出发地距离S(km)与行驶时间t(h)之间的函数关系的图象如图所示.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
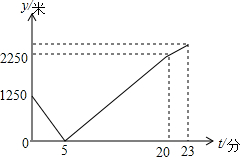 早晨,小刚沿着通往学校唯一的一条路(直路)上学,途中发现忘带饭盒,停下往家里打电话,妈妈接到电话后带上饭盒马上赶往学校,同时小刚返回,两人相遇后,小刚立即赶往学校,妈妈回家,15分钟妈妈到家,再经过3分钟小刚到达学校,小刚始终以100米/分的速度步行,小刚和妈妈的距离y(单位:米)与小刚打完电话后的步行时间t(单位:分)之间的函数关系如图,下列四种说法:
早晨,小刚沿着通往学校唯一的一条路(直路)上学,途中发现忘带饭盒,停下往家里打电话,妈妈接到电话后带上饭盒马上赶往学校,同时小刚返回,两人相遇后,小刚立即赶往学校,妈妈回家,15分钟妈妈到家,再经过3分钟小刚到达学校,小刚始终以100米/分的速度步行,小刚和妈妈的距离y(单位:米)与小刚打完电话后的步行时间t(单位:分)之间的函数关系如图,下列四种说法:查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,点O是等边三角形ABC内一点,已知∠AOB=115°,∠BOC=125°,则在以线段OA,OB,OC为边构成的三角形中,内角不可能取到的角度是( )
如图,点O是等边三角形ABC内一点,已知∠AOB=115°,∠BOC=125°,则在以线段OA,OB,OC为边构成的三角形中,内角不可能取到的角度是( )| A. | 65° | B. | 60° | C. | 55° | D. | 50° |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
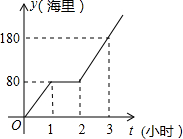 我国边防海警按照计划指定海域去巡逻,某巡逻艇匀速行驶一段时间后,因中途出现故障耽搁了一段时间,故障排除后,该艇加快速度仍匀速前进,结果恰好准点到达,如图是该艇行驶的路程y(海里)与所用时间t(小时)之间的函数图象,求该巡逻艇原计划准点到达指定海域所要行驶的路程.
我国边防海警按照计划指定海域去巡逻,某巡逻艇匀速行驶一段时间后,因中途出现故障耽搁了一段时间,故障排除后,该艇加快速度仍匀速前进,结果恰好准点到达,如图是该艇行驶的路程y(海里)与所用时间t(小时)之间的函数图象,求该巡逻艇原计划准点到达指定海域所要行驶的路程.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{1}{6}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{4}$ | D. | $\frac{5}{12}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com