
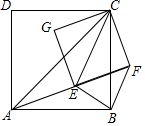
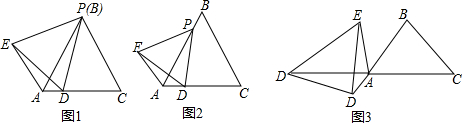
 如图,四边形ABCD,和四边形CFEG都是正方形,连接AC、AE、BF、CE.
如图,四边形ABCD,和四边形CFEG都是正方形,连接AC、AE、BF、CE.分析 (1)由四边形ABCD、四边形EFCG都是正方形,推出AC=$\sqrt{2}$BC,EC=$\sqrt{2}$CF,∠ACB=∠ECF,可得$\frac{AC}{EC}$=$\frac{EC}{CF}$=$\sqrt{2}$,∠ACE=∠BCF,由此即可证明;
(2)由△APC∽△BPF,推出$\frac{PA}{PB}$=$\frac{PC}{PF}$,即$\frac{PB}{PF}$=$\frac{PA}{PC}$,由△PCE∽△PAC,推出$\frac{PC}{PA}$=$\frac{PE}{PC}$,即$\frac{PA}{PC}$=$\frac{PC}{PE}$,可得$\frac{PB}{PF}$=$\frac{PC}{PE}$,由此即可解决问题;
(3)由△ACE∽△BCF,推出∠CAE=∠CBF,AE:BF=AC:BC=$\sqrt{2}$,由∠CBE+∠CAE=90°,AE=2,BE=1,推出∠CBE+∠CBF=90°,BF=$\sqrt{2}$,推出∠EBF=90°,可得EF=$\sqrt{{1}^{2}+(\sqrt{2})^{2}}$=$\sqrt{3}$,根据EC=$\sqrt{2}$EF计算即可;
解答 (1)证明:如图1中,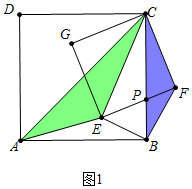
∵四边形ABCD、四边形EFCG都是正方形,
∴AC=$\sqrt{2}$BC,EC=$\sqrt{2}$CF,∠ACB=∠ECF,
∴$\frac{AC}{EC}$=$\frac{EC}{CF}$=$\sqrt{2}$,∠ACE=∠BCF,
∴△ACE∽△BCF,
(2)如图2中,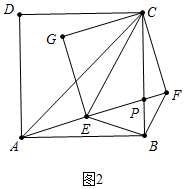
∵△ACE∽△BCF,
∴∠CAP=∠FBP,∵∠APC=∠BPF,
∴△APC∽△BPF,
∴$\frac{PA}{PB}$=$\frac{PC}{PF}$,
∴$\frac{PB}{PF}$=$\frac{PA}{PC}$,
∵∠APC=∠CPE,∠PEC=∠ACP=45°,
∴△PCE∽△PAC,
∴$\frac{PC}{PA}$=$\frac{PE}{PC}$,即$\frac{PA}{PC}$=$\frac{PC}{PE}$,
∴$\frac{PB}{PF}$=$\frac{PC}{PE}$,
∴PB•PE=PF•PC.
(3)如图3中,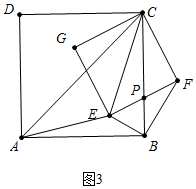
∵△ACE∽△BCF,
∴∠CAE=∠CBF,AE:BF=AC:BC=$\sqrt{2}$,
∵∠CBE+∠CAE=90°,AE=2,BE=1,
∴∠CBE+∠CBF=90°,BF=$\sqrt{2}$,
∴∠EBF=90°,
∴EF=$\sqrt{{1}^{2}+(\sqrt{2})^{2}}$=$\sqrt{3}$,
∴EC=$\sqrt{2}$EF=$\sqrt{6}$.
点评 本题考查相似三角形的性质、正方形的性质、等腰直角三角形的性质、勾股定理等知识,解题的关键是正确寻找相似三角形的相似条件,灵活运用所学知识看解决问题,属于中考压轴题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{12}{13}$ | B. | $\frac{5}{12}$ | C. | $\frac{13}{5}$ | D. | $\frac{5}{13}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 一艘轮船位于灯塔P南偏西60°方向上的点A处,在A正东方向上距离20海里的有一点B处,在灯塔P南偏西45°方向上,求A距离灯塔P的距离.
一艘轮船位于灯塔P南偏西60°方向上的点A处,在A正东方向上距离20海里的有一点B处,在灯塔P南偏西45°方向上,求A距离灯塔P的距离.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com