
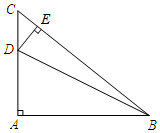
 如图,在等腰Rt△ABC中,∠A=90°,AC=6,D是AC上一点,过D作DE⊥BC于点E,若$tan∠DBA=\frac{1}{5}$,则CE的长为$\frac{12\sqrt{2}}{5}$.
如图,在等腰Rt△ABC中,∠A=90°,AC=6,D是AC上一点,过D作DE⊥BC于点E,若$tan∠DBA=\frac{1}{5}$,则CE的长为$\frac{12\sqrt{2}}{5}$. 分析 根据等腰直角三角形的性质得到AB=AC=6,∠C=∠B=45°,根据三角函数的定义得到AD=$\frac{6}{5}$,求得CD=$\frac{24}{5}$,解直角三角形得到结论.
解答 解:在等腰Rt△ABC中,∠A=90°,AC=6,
∴AB=AC=6,∠C=∠B=45°,
∵$tan∠DBA=\frac{1}{5}$,
∴AD=$\frac{6}{5}$,
∴CD=$\frac{24}{5}$,
∵DE⊥BC,
∴CE=$\frac{\sqrt{2}}{2}$CD=$\frac{12\sqrt{2}}{5}$,
故答案为:$\frac{12\sqrt{2}}{5}$.
点评 本题考查了解直角三角形:在直角三角形中,由已知元素求未知元素的过程就是解直角三角形.也考查了等腰直角三角形的性质.


 寒假乐园北京教育出版社系列答案
寒假乐园北京教育出版社系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 5 | B. | 6 | C. | 7 | D. | 10 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\left\{\begin{array}{l}{x+y=5}\\{z+x=3}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{x+\frac{1}{y}=1}\\{\frac{1}{x}-y=3}\end{array}\right.$ | ||
| C. | $\left\{\begin{array}{l}{x-y+xy=4}\\{3x-y=4}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{\frac{1}{2}x-2y=15}\\{\frac{1}{3}x+\frac{1}{2}y=4}\end{array}\right.$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
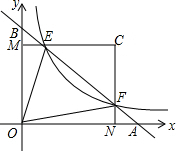 如图,在平面直角坐标系中,直线AB与x轴、y轴分别交于点A,B,与反比例函数 y=$\frac{k}{x}$(k为常数,且k>0)在第一象限的图象交于点E,F.过点E作EM⊥y轴于M,过点F作FN⊥x轴于N,直线EM与FN交于点C.若 $\frac{BE}{BF}$=$\frac{1}{4}$,记△CEF的面积为s1,△OEF的面积为s2,则 $\frac{s_1}{s_2}$=( )
如图,在平面直角坐标系中,直线AB与x轴、y轴分别交于点A,B,与反比例函数 y=$\frac{k}{x}$(k为常数,且k>0)在第一象限的图象交于点E,F.过点E作EM⊥y轴于M,过点F作FN⊥x轴于N,直线EM与FN交于点C.若 $\frac{BE}{BF}$=$\frac{1}{4}$,记△CEF的面积为s1,△OEF的面积为s2,则 $\frac{s_1}{s_2}$=( )| A. | $\frac{1}{4}$ | B. | $\frac{1}{2}$ | C. | $\frac{3}{5}$ | D. | $\frac{5}{8}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 小东到学校参加毕业晚会演出,到学校时发现演出道具还放在家中,此时距毕业晚会开始还有25分钟,于是立即步行回家.同时,他父亲从家里出发骑自行车以他3倍的速度给他送道具,两人在途中相遇,相遇后,小东父亲立即骑自行车以原来的速度载小东返回学校.图中线段AB、OB表示相遇前(含相遇)父亲送道具、小东取道具过程中,各自离学校的路程S(米)与所用时间t分)之间的函数关系,结合图象解答下列问题.
小东到学校参加毕业晚会演出,到学校时发现演出道具还放在家中,此时距毕业晚会开始还有25分钟,于是立即步行回家.同时,他父亲从家里出发骑自行车以他3倍的速度给他送道具,两人在途中相遇,相遇后,小东父亲立即骑自行车以原来的速度载小东返回学校.图中线段AB、OB表示相遇前(含相遇)父亲送道具、小东取道具过程中,各自离学校的路程S(米)与所用时间t分)之间的函数关系,结合图象解答下列问题.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,下列三个条件:①AB∥CD,②∠B=∠C,③∠E=∠F.
如图,下列三个条件:①AB∥CD,②∠B=∠C,③∠E=∠F.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com