
【题目】如图,直线AB分别交y轴、x轴于A、B两点,OA=2,tan∠ABO= ![]() ,抛物线y=﹣x2+bx+c过A、B两点.
,抛物线y=﹣x2+bx+c过A、B两点.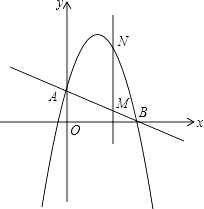
(1)求直线AB和这个抛物线的解析式;
(2)设抛物线的顶点为D,求△ABD的面积;
(3)作垂直x轴的直线x=t,在第一象限交直线AB于M,交这个抛物线于N.求当t取何值时,MN的长度l有最大值?最大值是多少?
【答案】
(1)
解:∵在Rt△AOB中,tan∠ABO= ![]() ,OA=2,
,OA=2,
即 ![]() =
= ![]() ,
,
∴0B=4,
∴A(0,2),B(4,0),
把A、B的坐标代入y=﹣x2+bx+c得: ![]() ,
,
解得:b= ![]() ,
,
∴抛物线的解析式为y=﹣x2+ ![]() x+2,
x+2,
设直线AB的解析式为y=kx+e,把A、B的坐标代入得: ![]() ,
,
解得:k=﹣ ![]() ,e=2,
,e=2,
所以直线AB的解析式是y=﹣ ![]() x+2
x+2
(2)
解:过点D作DE⊥y轴于点E,
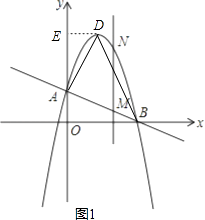
由(1)抛物线解析式为y=﹣x2+ ![]() x+2=﹣(x﹣
x+2=﹣(x﹣ ![]() )2+
)2+ ![]() ,
,
即D的坐标为( ![]() ,
, ![]() ),
),
则ED= ![]() ,EO=
,EO= ![]() ,
,
AE=EO﹣OA= ![]() ,
,
S△ABD=S梯形DEOB﹣S△DEA﹣S△AOB= ![]() ×(
×( ![]() +4)×
+4)× ![]() ﹣
﹣ ![]() ×
× ![]() ﹣
﹣ ![]() ×4×2=
×4×2= ![]()
(3)
解:由题可知,M、N横坐标均为t.
∵M在直线AB:y=﹣ ![]() x+2上
x+2上
∴M(t,﹣ ![]() t+2)
t+2)
∵N在抛物线y=﹣x2+ ![]() x+2上
x+2上
∴M(t,﹣t2+ ![]() t+2),
t+2),
∵作垂直x轴的直线x=t,在第一象限交直线AB于M,交这个抛物线于N,
∴MN=﹣t2+ ![]() t+2﹣(﹣
t+2﹣(﹣ ![]() +2)=﹣t2+4t=﹣(t﹣2)2+4,
+2)=﹣t2+4t=﹣(t﹣2)2+4,
其中0<t<4,
∴当t=2时,MN最大=4,
所以当t=2时,MN的长度l有最大值,最大值是4
【解析】(1)求出OB,把A、B的坐标代入y=﹣x2+bx+c和y=kx+e求出即可;(2)求出D的坐标,再根据面积公式求出即可;(3)求出M、N的坐标,求出MN的值,再化成顶点式,即可求出答案.


 星级口算天天练系列答案
星级口算天天练系列答案 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案科目:初中数学 来源: 题型:
【题目】为减少环境污染,自2008年6月1日起,全国的商品零售场所开始实行“塑料购物袋有偿使用制度”(以下简称“限塑令”).某班同学于6月上旬的一天,在某超市门口采用问卷调查的方式,随机调查了“限塑令”实施前后,顾客在该超市用购物袋的情况,以下是根据100位顾客的100份有效答卷画出的统计图表的一部分: 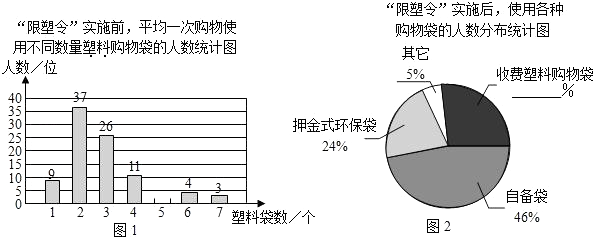
“限塑令”实施后,塑料购物袋使用后的处理方式统计表:
处理方式 | 直接丢弃 | 直接做垃圾袋 | 再次购物使用 | 其它 |
选该项的人数占 | 5% | 35% | 49% | 11% |
请你根据以上信息解答下列问题:
(1)补全图1,“限塑令”实施前,如果每天约有2 000人次到该超市购物.根据这100位顾客平均一次购物使用塑料购物袋的平均数,估计这个超市每天需要为顾客提供多少个塑料购物袋?
(2)补全图2,并根据统计图和统计表说明,购物时怎样选用购物袋,塑料购物袋使用后怎样处理,能对环境保护带来积极的影响.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,∠B=∠D=60°,∠BAC=∠ACD=90°,点E为边AB上一点,AB=3AE=3cm,动点P从B点出发,以1cm/s的速度沿BC→CD→DA运动至A点停止,设运动时间为t秒.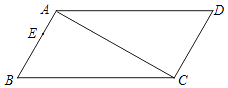
(1)求证四边形ABCD是平行四边形;
(2)当△BEP为等腰三角形时,求t2﹣31t的值;
(3)当t=4时,把△ABP沿直线AP翻折,得到△AFP,求△AFP与ABCD重叠部分的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,点C是线段AB上的一点,点D是线段AB的中点,点E是线段BC的中点.
![]()
(1)当AC=10,BC=8时,求线段DE的长度;
(2)当AC=m,BC=n(m>n)时,求线段DE的长度;
(3)从(1)(2)的结果中,你发现了什么规律?请直接写出来.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为增强公民的节约意识,合理利用天然气资源,某市自1月1日起对市区民用管道天然气价格进行调整,实行阶梯式气价,调整后的收费价格如表所示:
每月用气量 | 单价(元/m3) |
不超出80m3的部分 | 2.5 |
超出80m3不超出130m3的部分 | a |
超出130m3的部分 | a+0.5 |
(1)若甲用户3月份用气125m3,缴费335元,求a的值;
(2)在(1)的条件下,若乙用户3月份缴费392元,则乙用户3月份的用气量是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
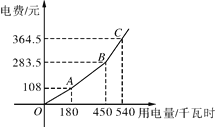
【题目】为了响应国家节能减排的号召,鼓励市民节约用电,我市从2012年7月1日起,居民用电实行“一户一表”的“阶梯电价”,分三个档次收费,第一档是用电量不超过180千瓦时实行“基本电价”,第二、三档实行“提高电价”,具体收费情况如图的折线图,请根据图象回答下列问题;
(1)当用电量是180千瓦时时,电费是__________元;
(2)第二档的用电量范围是__________;
(3)“基本电价”是__________元/千瓦时;
(4)小明家8月份的电费是328.5元,这个月他家用电多少千瓦时?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平行四边形ABCD中,E、F分别在AD、BC边上,且AE=CF.
求证:(1)△ABE≌△CDF;
(2)四边形BFDE是平行四边形.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】数轴上A 点对应的数为﹣5,B 点在A 点右边,电子蚂蚁甲、乙在B分别以2个单位/秒、1个单位/秒的速度向左运动,电子蚂蚁丙在A 以3个单位/秒的速度向右运动.
(1)若电子蚂蚁丙经过5秒运动到C 点,求C 点表示的数;
![]()
(2)若它们同时出发,若丙在遇到甲后1秒遇到乙,求B 点表示的数;
![]()
(3)在(2)的条件下,设它们同时出发的时间为t 秒,是否存在t的值,使丙到乙的距离是丙到甲的距离的2倍?若存在,求出t 值;若不存在,说明理由.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
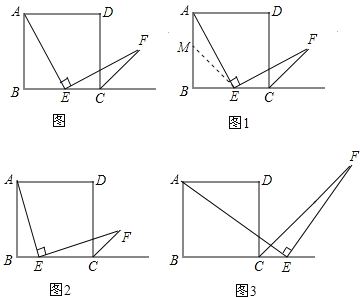
【题目】如图,四边形ABCD是正方形,点E是边BC的中点,∠AEF=90°,且EF交正方形外角平分线CF于点F.请你认真阅读下面关于这个图的探究片段,完成所提出的问题.
(1)探究1:小强看到图(*)后,很快发现AE=EF,这需要证明AE和EF所在的两个三角形全等,但△ABE和△ECF显然不全等(一个是直角三角形,一个是钝角三角形),考虑到点E是边BC的中点,因此可以选取AB的中点M,连接EM后尝试着去证△AEM≌EFC就行了,随即小强写出了如下的证明过程:
证明:如图1,取AB的中点M,连接EM.
∵∠AEF=90°
∴∠FEC+∠AEB=90°
又∵∠EAM+∠AEB=90°
∴∠EAM=∠FEC
∵点E,M分别为正方形的边BC和AB的中点
∴AM=EC
又可知△BME是等腰直角三角形
∴∠AME=135°
又∵CF是正方形外角的平分线
∴∠ECF=135°
∴△AEM≌△EFC(ASA)
∴AE=EF
(2)探究2:小强继续探索,如图2,若把条件“点E是边BC的中点”改为“点E是边BC上的任意一点”,其余条件不变,发现AE=EF仍然成立,请你证明这一结论.
(3)探究3:小强进一步还想试试,如图3,若把条件“点E是边BC的中点”改为“点E是边BC延长线上的一点”,其余条件仍不变,那么结论AE=EF是否成立呢?若成立请你完成证明过程给小强看,若不成立请你说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com