
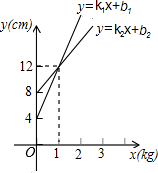 若甲、乙两弹簧的长度ycm与所挂物体质量xkg之间的函数表达式分别为y=k1x+b1和y=k2x+b2,如图所示,所挂物体质量均为2kg时,甲弹簧长为y1,乙弹簧长为y2,则y1与y2的大小关系为( )
若甲、乙两弹簧的长度ycm与所挂物体质量xkg之间的函数表达式分别为y=k1x+b1和y=k2x+b2,如图所示,所挂物体质量均为2kg时,甲弹簧长为y1,乙弹簧长为y2,则y1与y2的大小关系为( )| A. | y1>y2 | B. | y1=y2 | C. | y1<y2 | D. | 不能确定 |
分析 将点(0,4)和点(1,12)代入y1=k1x+b1中求出k1和b1,将点(0,8)和点(1,12)代入y2=k2x+b2中求出k2和b2,再将x=2代入两式比较y1和y2大小.
解答 解:∵点(0,4)和点(1,12)在y1=k1x+b1上,
∴得到方程组:$\left\{\begin{array}{l}{4={b}_{1}}\\{12={k}_{1}+{b}_{1}}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{{k}_{1}=8}\\{{b}_{1}=4}\end{array}\right.$,
∴y1=8x+4.
∵点(0,8)和点(1,12)代入y2=k2x+b2上,
∴得到方程组为$\left\{\begin{array}{l}{8={b}_{2}}\\{12={k}_{2}+{b}_{2}}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{{k}_{2}=4}\\{{b}_{2}=8}\end{array}\right.$.
∴y2=4x+8.
当x=2时,y1=8×2+4=20,y2=4×2+8=16,
∴y1>y2.
故选A.
点评 本题考查了一次函数的应用,待定系数法求一次函数关系式,比较函数值的大小,熟练掌握待定系数法求一次函数关系式是解题的关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
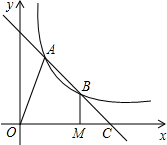 如图,直线AB交双曲线y=$\frac{k}{x}$于A、B,交x轴于点C,B为线段AC的中点,过点B作BM⊥x轴于M,连结OA.若OM=2MC,四边形OABM的面积为5,则k的值为( )
如图,直线AB交双曲线y=$\frac{k}{x}$于A、B,交x轴于点C,B为线段AC的中点,过点B作BM⊥x轴于M,连结OA.若OM=2MC,四边形OABM的面积为5,则k的值为( )| A. | 3 | B. | 4 | C. | 5 | D. | 6 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 已知:如图,在Rt△ABC中,∠ACB=90°,BC=6cm,AB=10cm.一动点M在边AC上从A向C以3cm/s的速度匀速运动,另一动点N在边BC上同时从C向B以2cm/s的速度匀速运动,当其中一个点到达终点时另一点也随之停止运动.设运动的时间为x秒.
已知:如图,在Rt△ABC中,∠ACB=90°,BC=6cm,AB=10cm.一动点M在边AC上从A向C以3cm/s的速度匀速运动,另一动点N在边BC上同时从C向B以2cm/s的速度匀速运动,当其中一个点到达终点时另一点也随之停止运动.设运动的时间为x秒.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图:A,B是函数y=$\frac{2}{x}$的图象上关于原点O点对称的任意两点,AC垂直于x轴于点C,BD垂直于y轴于点D,设四边形ADBC的面积为S,则( )
如图:A,B是函数y=$\frac{2}{x}$的图象上关于原点O点对称的任意两点,AC垂直于x轴于点C,BD垂直于y轴于点D,设四边形ADBC的面积为S,则( )| A. | S=2 | B. | 2<S<4 | C. | S=4 | D. | S>4 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 计算: (1)28+(-72) | (2)0+(-5) | (3)-$\frac{1}{5}$+(+$\frac{1}{6}$) |
| (4)(-3)-(-5) | (5)$({-3\frac{1}{2}})-5\frac{1}{4}$ | (6)(-8)+(-5)-(+5) |
| (7)-37-40+3-22 | (7)$(({-4})×({-\frac{3}{4}})×2$ | (8)(-5)×(-4)×3×(-2) |
| (9)-12÷$\frac{1}{4}÷({-\frac{8}{3}})$ | (10)$({\frac{1}{3}-\frac{5}{6}+\frac{7}{9}})÷({\frac{1}{18}})$ | (11)9$\frac{15}{16}×({-8})$ |
| (12)100÷$\frac{1}{8}×({-8})$ | (13)$1÷({-\frac{2}{7}})×\frac{1}{7}$ | (14)$\frac{1}{2}×({-\frac{4}{15}})÷\frac{2}{3}$. |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题

| A. | 2013 | B. | 2014 | C. | 2015 | D. | 2016 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com