
【题目】如图,在平面直角坐标系中,O为坐标原点,点A的坐标为(5,0),菱形OABC的顶点B,C都在第一象限,tan∠AOC= ![]() ,将菱形绕点A按顺时针方向旋转角α(0°<∠α<∠AOC)得到菱形FADE(点O的对应点为点F),EF与OC交于点G,连结AG.
,将菱形绕点A按顺时针方向旋转角α(0°<∠α<∠AOC)得到菱形FADE(点O的对应点为点F),EF与OC交于点G,连结AG. 
(1)求点B的坐标.
(2)当OG=4时,求AG的长.
(3)求证:GA平分∠OGE.
(4)连结BD并延长交x轴于点P,当点P的坐标为(12,0)时,求点G的坐标.
【答案】
(1)
解:如图1,过点B作BH⊥x轴于点H,
∵四边形OABC为菱形,
∴OC∥AB,
∴∠BAH=∠COA.
∵tan∠AOC= ![]() ,
,
∴tan∠BAH= ![]() .
.
又∵在直角△BAH中,AB=5,
∴BH= ![]() AB=4,AH=
AB=4,AH= ![]() AB=3,
AB=3,
∴OH=OA+AH=5+3=8,
∴点B的坐标为(8,4)
(2)
解:如图1,
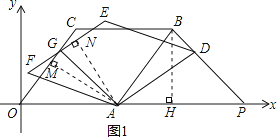
过点A作AM⊥OC于点M,
在直角△AOM中,∵tan∠AOC= ![]() ,OA=5,
,OA=5,
∴AM= ![]() OA=4,OM=
OA=4,OM= ![]() OA=3,
OA=3,
∵OG=4,
∴GM=OG﹣OM=4﹣3=1,
∴AG= ![]() =
= ![]() =
= ![]()
(3)
证明:如图1,

过点A作AN⊥EF于点N,
∵在△AOM与△AFN中, 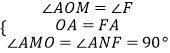 ,
,
∴△AOM≌△AFN(ASA),
∴AM=AN,
∴GA平分∠OGE
(4)
解:如图2,
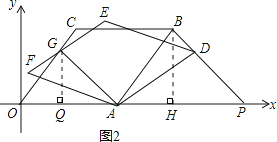
过点G作GQ⊥x轴于点Q,
由旋转可知:∠OAF=∠BAD=α.
∵AB=AD,
∴∠ABP= ![]() ,
,
∵∠AOT=∠F,∠OTA=∠GTF,
∴∠OGA=∠EGA= ![]() ,
,
∴∠OGA=ABP,
又∵∠GOA=∠BAP,
∴△GOA∽△BAP,
∴ ![]() ,
,
∴GQ= ![]() ×4=
×4= ![]() .
.
∵tan∠AOC= ![]() ,
,
∴OQ= ![]() ×
× ![]() =
= ![]() ,
,
∴G( ![]() ,
, ![]() ).
).
【解析】(1)如图1,过点B作BH⊥x轴于点H,构建直角△ABH,所以利用菱形的四条边相等的性质和解该直角三角形得到AH、BH的长度,则易求点B的坐标;(2)如图1,过点A作AM⊥OC于点M,构建直角△OAM和直角△AMG,通过解直角△OAM求得直角边AM的长度,然后结合图形和勾股定理来求AG的长度;(3)如图1,过点A作AM⊥OC于点M,构建全等三角形:△AOM≌△AFN(ASA),利用该全等三角形的对应边相等得到AM=AN,最后结合角平分线的性质证得结论;(4)如图2,过点G作GQ⊥x轴于点Q,构建相似三角形:△GOA∽△BAP,根据该相似三角形的对应边成比例得到求得GQ的长度.结合已知条件tan∠AOC= ![]() ,来求边OQ的长度,即可得到点G的坐标.本题考查了四边形综合题.解题过程中,涉及到了全等三角形的判定与性质,相似三角形的判定与性质,旋转的性质,解直角三角形以及勾股定理等知识点,解答该题的难点在于作出辅助线,构建相关的图形的性质.
,来求边OQ的长度,即可得到点G的坐标.本题考查了四边形综合题.解题过程中,涉及到了全等三角形的判定与性质,相似三角形的判定与性质,旋转的性质,解直角三角形以及勾股定理等知识点,解答该题的难点在于作出辅助线,构建相关的图形的性质.
【考点精析】解答此题的关键在于理解勾股定理的概念的相关知识,掌握直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2,以及对相似三角形的判定与性质的理解,了解相似三角形的一切对应线段(对应高、对应中线、对应角平分线、外接圆半径、内切圆半径等)的比等于相似比;相似三角形周长的比等于相似比;相似三角形面积的比等于相似比的平方.


科目:初中数学 来源: 题型:
【题目】如图,直线y=﹣ ![]() 与x轴、y轴分别交于点A、B;点Q是以C(0,﹣1)为圆心、1为半径的圆上一动点,过Q点的切线交线段AB于点P,则线段PQ的最小是 .
与x轴、y轴分别交于点A、B;点Q是以C(0,﹣1)为圆心、1为半径的圆上一动点,过Q点的切线交线段AB于点P,则线段PQ的最小是 . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下表是某校合唱团成员的年龄分布
年龄/岁 | 13 | 14 | 15 | 16 |
频数 | 5 | 15 | x | 10﹣x |
对于不同的x,下列关于年龄的统计量不会发生改变的是( )
A.平均数、中位数
B.众数、中位数
C.平均数、方差
D.中位数、方差
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠B=90°,tan∠C= ![]() ,AB=6cm.动点P从点A开始沿边AB向点B以1cm/s的速度移动,动点Q从点B开始沿边BC向点C以2cm/s的速度移动.若P,Q两点分别从A,B两点同时出发,在运动过程中,△PBQ的最大面积是( )
,AB=6cm.动点P从点A开始沿边AB向点B以1cm/s的速度移动,动点Q从点B开始沿边BC向点C以2cm/s的速度移动.若P,Q两点分别从A,B两点同时出发,在运动过程中,△PBQ的最大面积是( )
A.18cm2
B.12cm2
C.9cm2
D.3cm2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】济南大明湖畔的“超然楼”被称作“江北第一楼”,某校数学社团的同学对超然楼的高度进行了测量,如图,他们在A处仰望塔顶,测得仰角为30°,再往楼的方向前进60m至B处,测得仰角为60°,若学生的身高忽略不计, ![]() ≈1.7,结果精确到1m,则该楼的高度CD为( )
≈1.7,结果精确到1m,则该楼的高度CD为( ) 
A.47m
B.51m
C.53m
D.54m
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】圆桌面(桌面中间有一个直径为0.4m的圆洞)正上方的灯泡(看作一个点)发出的光线照射平行于地面的桌面后,在地面上形成如图所示的圆环形阴影.已知桌面直径为1.2m,桌面离地面1m,若灯泡离地面3m,则地面圆环形阴影的面积是( ) 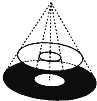
A.0.324πm2
B.0.288πm2
C.1.08πm2
D.0.72πm2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=x2﹣2x﹣8交y轴于点A,交x轴正半轴于点B.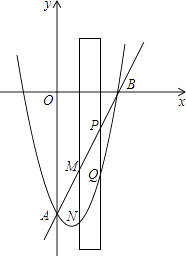
(1)求直线AB对应的函数关系式;
(2)有一宽度为1的直尺平行于y轴,在点A、B之间平行移动,直尺两长边所在直线被直线AB和抛物线截得两线段MN、PQ,设M点的横坐标为m,且0<m<3.试比较线段MN与PQ的大小.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com