
ЁОЬтФПЁПаЁРюОгЊЕФГЕЪЮЕъЯњЪлФГЦЗХЦГЕЦсаоИДвКЃЌвбжЊЦфНјМлЮЊ40дЊ/жЇЃЌЪдЯњНзЖЮЗЂЯжНЋЪлМлЖЈЮЊ80дЊ/жЇЪБЃЌУПЬьПЩЯњЪл20жЇЃЌКѓРДЮЊСЫРЉДѓЯњЪлСПЃЌаЁРюЪЪЕБНЕЕЭСЫЪлМлЃЌЯњЪлСПyЃЈжЇЃЉгыНЕМлxЃЈдЊЃЉЕФЙиЯЕШчЭМЫљЪОЃЎ
ЃЈ1ЃЉЧызаЯИЖСЬтЃЌВЂВЙШЋЯТУцБэИёЃК
НЕМлx/дЊ | Ё | 2 | 4 | ЁЁ ЁЁ | x | Ё |
ЯњСПy/жЇ | Ё | 24 | 28 | 30 | ЁЁ ЁЁ | Ё |
ЃЈ2ЃЉШєвЊЪЙЕУЦНОљУПЬьЯњЪлетжжаоИДвКЕФРћШѓWзюДѓЃЌдђУПжЇаоИДвКгІИУНЕМлЖрЩйдЊЃПзюДѓЕФРћШѓWЮЊЖрЩйдЊЃП
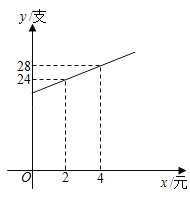
ЁОД№АИЁПЃЈ1ЃЉ5ЃЌ2x+20ЃЛЃЈ2ЃЉЕБУПжЇНЕМл15дЊЪБЃЌШеЯњЪлРћШѓзюДѓЮЊ1250дЊЃЎ
ЁОНтЮіЁП
ЃЈ1ЃЉЪзЯШРћгУД§ЖЈЯЕЪ§ЗЈШЗЖЈвЛДЮКЏЪ§ЕФНтЮіЪНЃЌШЛКѓДњШыxЛђyЕФжЕЧѓЕУyЛђxЕФжЕМДПЩЃЛ
ЃЈ2ЃЉИљОнЬтвтСаГіЖўДЮКЏЪ§ЃЌЧѓЕУКЏЪ§ЕФзюжЕМДПЩЧѓНтД№АИЃЎ
НтЃКЃЈ1ЃЉЩшyгыxЕФКЏЪ§ЙиЯЕЪНЮЊyЃНkx+bЃЌ
гЩКЏЪ§ЭМЯѓПЩСаЗНГЬзщЃК![]() ЃЌ
ЃЌ
НтЕУЃК![]() ЃЌ
ЃЌ
ЁрyгыxЕФКЏЪ§ЙиЯЕЪНЮЊyЃН2x+20ЃЛ
ЕБyЃН30ЪБЃЌ30ЃН2x+20ЃЌЕУЃКxЃН5ЃЌ
ВЙШЋБэИёШчЯТЃК
НЕМлx/дЊ | Ё | 2 | 4 | 5 | x | Ё |
ЯњСПy/жЇ | Ё | 24 | 28 | 30 | 2x+20 | Ё |
ЙЪД№АИЮЊЃК5ЃЌ2x+20ЃЛ
ЃЈ2ЃЉЩшНЕМлxдЊЃЌдђУПжЇГЕЦсаоИДвКЕФРћШѓЮЊЃЈ80ЉxЉ40ЃЉЃЌЯњЪлЕФЪ§СПЮЊyЃЌ
ЙЪУПЬьЕФЯњЪлРћШѓWЃНЃЈ80Љ40ЉxЃЉЃЈ2x+20ЃЉЃНЉ2ЃЈxЉ15ЃЉ2+1250ЃЌ
ЁпaЃНЉ2ЃМ0ЃЌ
ЁрЕБxЃН15ЪБЃЌWгазюДѓжЕЮЊ1250ЃЎ
ЁрЕБУПжЇНЕМл15дЊЪБЃЌШеЯњЪлРћШѓзюДѓЮЊ1250дЊЃЎ



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкЦНУцжБНгзјБъЯЕжаЃЌНЋЗДБШР§КЏЪ§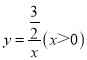 ЕФЭМЯѓШЦзјБъдЕуOФцЪБеыа§зЊ45ЁуЕУЕНЕФЧњЯпlЃЌЙ§Еу
ЕФЭМЯѓШЦзјБъдЕуOФцЪБеыа§зЊ45ЁуЕУЕНЕФЧњЯпlЃЌЙ§Еу![]() ЃЌ
ЃЌ![]()
![]() ЕФжБЯпгыЧњЯпlЯрНЛгкЕуCЁЂDЃЌдђsinЁЯCOD=___ ЃЎ
ЕФжБЯпгыЧњЯпlЯрНЛгкЕуCЁЂDЃЌдђsinЁЯCOD=___ ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
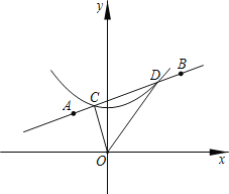
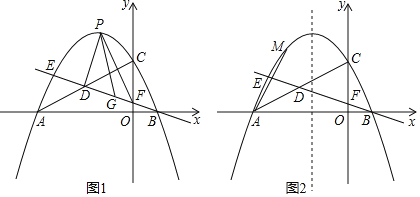
ЁОЬтФПЁПШчЭМ1ЃЌХзЮяЯп![]() гыxжсНЛгкAЃЌBСНЕуЃЌгыyжсНЛгкЕуCЃЌЕуDЮЊЯпЖЮACЕФжаЕуЃЌжБЯпBDгыХзЮяЯпНЛгкСэвЛЕуEЃЌгыyжсНЛгкЕуFЃЎ
гыxжсНЛгкAЃЌBСНЕуЃЌгыyжсНЛгкЕуCЃЌЕуDЮЊЯпЖЮACЕФжаЕуЃЌжБЯпBDгыХзЮяЯпНЛгкСэвЛЕуEЃЌгыyжсНЛгкЕуFЃЎ
(1)ШчЭМ1ЃЌЕуPЪЧжБЯпBEЩЯЗНХзЮяЯпЩЯвЛЖЏЕуЃЌСЌНгPDЃЌPFЃЌЕБЁїPDFЕФУцЛ§зюДѓЪБЃЌдкЯпЖЮBEЩЯеввЛЕуGЃЌЪЙЕУPGЉ![]() EGЕФжЕзюаЁЃЌЧѓГіPGЉ
EGЕФжЕзюаЁЃЌЧѓГіPGЉ![]() EGЕФзюаЁжЕЃЛ
EGЕФзюаЁжЕЃЛ
(2)ШчЭМ2ЃЌЕуMЮЊХзЮяЯпЩЯвЛЕуЃЌЕуNдкХзЮяЯпЕФЖдГЦжсЩЯЃЌЕуKЮЊЦНУцФквЛЕуЃЌЕБвдЕуAЁЂMЁЂNЁЂKЮЊЖЅЕуЕФЫФБпаЮЪЧе§ЗНаЮЪБЃЌжБНгаДГіЕуNЕФзјБъЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПФГЕчЪгЬЈЕФвЛЕЕгщРжадНкФПжаЃЌдкгЮЯЗPKЛЗНкЃЌЮЊСЫЫцЛњЗжбЁгЮЯЗЫЋЗНЕФзщдБЃЌжїГжШЫЩшМЦСЫвдЯТгЮЯЗЃКгУВЛЭИУїЕФАзВМАќзЁШ§ИљбеЩЋГЄЖЬЯрЭЌЕФЯИЩўAA1ЁЂBB1ЁЂCC1ЃЌжЛТЖГіЫќУЧЕФЭЗКЭЮВЃЈШчЭМЫљЪОЃЉЃЌгЩМзЁЂввСНЮЛМЮБіЗжБ№ДгАзВМСНЖЫИїбЁвЛИљЯИЩўЃЌВЂРГіЃЌШєСНШЫбЁжаЭЌвЛИљЯИЩўЃЌдђСНШЫЭЌЖгЃЌЗёдђЛЅЮЊЗДЗНЖгдБЃЎ
ЃЈ1ЃЉШєМзМЮБіДгжаШЮвтбЁдёвЛИљЯИЩўРГіЃЌЧѓЫћЧЁКУГщГіЯИЩўAA1ЕФИХТЪЃЛ
ЃЈ2ЃЉЧыгУЛЪїзДЭМЗЈЛђСаБэЗЈЃЌЧѓМзЁЂввСНЮЛМЮБіФмЗжЮЊЭЌЖгЕФИХТЪЃЎ
![]()
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
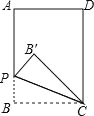
ЁОЬтФПЁПШчЭМЃЌдкОиаЮABCDжаЃЌAB=4ЃЌBC=3ЃЌЕуPЪЧABЩЯЃЈВЛКЌЖЫЕуAЃЌBЃЉШЮвтвЛЕуЃЌАбЁїPBCбиPCелЕўЃЌЕБЕуBЁфЕФЖдгІЕуТфдкОиаЮABCDЕФЖдНЧЯпЩЯЪБЃЌBP=__________________________ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁП ЁАвЫОгГЄЩГЁБЪЧЮвУЧЕФЙВЭЌдИОАЃЌПеЦјжЪСПБЖЪмШЫУЧЕФЙизЂЃЎЮвЪаФГПеЦјжЪСПМьВтеОЕуМьВтСЫИУЧјгђУПЬьЕФПеЦјжЪСПЧщПіЃЌЭГМЦСЫ2013Фъ1дТЗнжС4дТЗнШєИЩЬьЕФПеЦјжЪСПЧщПіЃЌВЂЛцжЦСЫШчЯТСНЗљВЛЭъећЕФЭГМЦЭМЃЌЧыИљОнЭМжааХЯЂЃЌНтД№ЯТСаЮЪЬтЃК
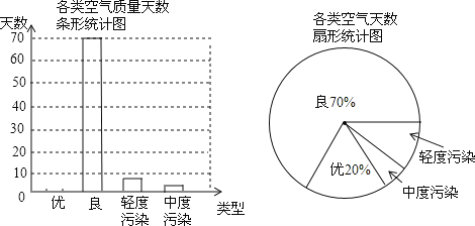
ЃЈ1ЃЉЭГМЦЭМЙВЭГМЦСЫ______ЬьПеЦјжЪСПЧщПіЃЎ
ЃЈ2ЃЉЧыНЋЬѕаЮЭГМЦЭМВЙГфЭъећЃЌВЂМЦЫуПеЦјжЪСПЮЊЁАгХЁБЫљдкЩШаЮдВаФНЧЖШЪ§ЃЎ
ЃЈ3ЃЉДгаЁдДЫљдкАрМЖЕФ40УћЭЌбЇжаЃЌЫцЛњбЁШЁвЛУћЭЌбЇШЅИУПеЦјжЪСПМрВтЕуВЮЙлЃЌдђЧЁКУбЁЕНаЁдДЕФИХТЪЪЧЖрЩйЃП
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌвбжЊЕуAЃЌBЕФзјБъЗжБ№ЮЊЃЈ4ЃЌ0ЃЉЃЌЃЈ3ЃЌ2ЃЉЃЎ
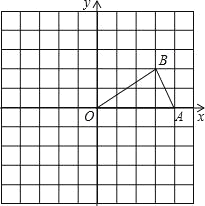
ЃЈ1ЃЉЛГіЁїAOBЙигкдЕуOЖдГЦЕФЭМаЮЁїCODЃЛ
ЃЈ2ЃЉНЋЁїAOBШЦЕуOАДФцЪБеыЗНЯђа§зЊ90ЁуЕУЕНЁїEOFЃЌЛГіЁїEOFЃЛ
ЃЈ3ЃЉЕуDЕФзјБъЪЧЁЁ ЁЁЃЌЕуFЕФзјБъЪЧЁЁ ЁЁЃЌДЫЭМжаЯпЖЮBFКЭDFЕФЙиЯЕЪЧЁЁ ЁЁЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
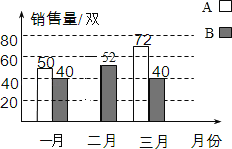
ЁОЬтФПЁПвЄЙЕДхЖдЕквЛМОЖШAЁЂBСНжжЫЎЙћЕФЯњЪлЧщПіНјааЭГМЦЃЌСНжжЫЎЙћЕФЯњЪлСПШчЭМЫљЪОЃЎ
ЃЈ1ЃЉЕквЛМОЖШBжжЫЎЙћЕФдТЦНОљЯњЪлСПЪЧЖрЩйЖжЃП
ЃЈ2ЃЉвЛдТAжжЫЎЙћЕФЯњЪлСПЪЧ50ЖжЃЌЕНШ§дТAжжЫЎЙћЕФЯњЪлСПЪЧ72ЖжЃЌЕквЛМОЖШAжжЫЎЙћЕФЯњЪлСПЕФдТЦНОљдіГЄТЪЯрЭЌЃЌЧѓЖўдТAжжЫЎЙћЯњЪлСЫЖрЩйЖжЃП
ЃЈ3ЃЉИљОнвдЩЯаХЯЂЃЌЧыНЋЭГМЦЭМВЙГфЭъећЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌЁїABCжаЃЌEЪЧACЩЯвЛЕуЃЌЧвAE=ABЃЌЁЯBAC=2ЁЯEBC ЃЌвдABЮЊжБОЖЕФЁбOНЛACгкЕуDЃЌНЛEBгкЕуFЃЎ
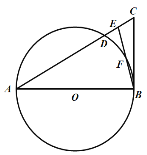
ЃЈ1ЃЉЧѓжЄЃКBCгыЁбOЯрЧаЃЛ
ЃЈ2ЃЉШєAB=8ЃЌBE=4ЃЌЧѓBCЕФГЄЃЎ
ВщПДД№АИКЭНтЮі>>
АйЖШжТаХ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com