
(本题满分10分)抛物线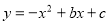 与x轴交与
与x轴交与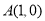 ,
,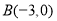 两点,
两点,
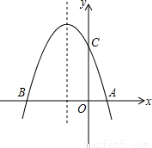
(1)求该抛物线的解析式;
(2)设(1)中的抛物线与y轴交于C点,在该抛物线的对称轴上是否存在点Q,使得△QAC的周长最小?若存在,求出Q点的坐标;若不存在,请说明理由.
(1)y=-x2-2x+3;(2)存在Q(-1,2).
【解析】
试题分析:(1)把A(1,0)B(-3,0)代入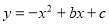 然后解方程组即可;(2)因为线段AC的长固定不变,所以当AQ+CQ的长最小时△QAC的周长最小,根据轴对称的性质可知直线BC与对称轴的交点即为Q点,用待定系数法求直线BC解析式,把对称轴x=-1代入即可.
然后解方程组即可;(2)因为线段AC的长固定不变,所以当AQ+CQ的长最小时△QAC的周长最小,根据轴对称的性质可知直线BC与对称轴的交点即为Q点,用待定系数法求直线BC解析式,把对称轴x=-1代入即可.
试题解析:解(1)把A(1,0)B(-3,0)代入到
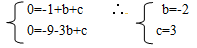 3分
3分
∴抛物线的解析式为y=-x2-2x+3 5分
(2)存在。 6分
过B、C作直线BC与对称轴x=-1的交点就是Q点,
设直线BC解析式为y=kx+b,把B(-3,0)C(0,3)代入到
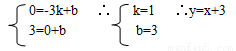
令XQ=-1 得YQ=2 ∴Q(-1,2) 10分
考点:1.待定系数法求函数解析式;2. 轴对称的性质.
考点分析: 考点1:二次函数 定义: (a,b,c是常数,a≠0),那么y叫做x 的二次函数。
(a,b,c是常数,a≠0),那么y叫做x 的二次函数。  (a≠0)中x、y是变量,a,b,c是常数,自变量x 的取值范围是全体实数,b和c可以是任意实数,a是不等于0的实数,因为a=0时,
(a≠0)中x、y是变量,a,b,c是常数,自变量x 的取值范围是全体实数,b和c可以是任意实数,a是不等于0的实数,因为a=0时, 变为y=bx+c若b≠0,则y=bx+c是一次函数,若b=0,则y=c是一个常数函数。
变为y=bx+c若b≠0,则y=bx+c是一次函数,若b=0,则y=c是一个常数函数。 (a≠0)与一元二次方程
(a≠0)与一元二次方程 (a≠0)有密切联系,如果将变量y换成一个常数,那么这个二次函数就是一个一元二次函数。
二次函数的解析式有三种形式:
(a≠0)有密切联系,如果将变量y换成一个常数,那么这个二次函数就是一个一元二次函数。
二次函数的解析式有三种形式:  (a,b,c是常数,a≠0);
(a,b,c是常数,a≠0);  (a,h,k是常数,a≠0)
(a,h,k是常数,a≠0)  与x轴有交点时,即对应二次好方程
与x轴有交点时,即对应二次好方程 有实根x1和x2存在时,根据二次三项式的分解因式
有实根x1和x2存在时,根据二次三项式的分解因式 ,二次函数
,二次函数 可转化为两根式
可转化为两根式 。如果没有交点,则不能这样表示。
。如果没有交点,则不能这样表示。  (a≠0)的形式,那么这个函数就是二次函数,否则就不是。
试题属性
(a≠0)的形式,那么这个函数就是二次函数,否则就不是。
试题属性


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源:2014-2015学年山东省滕州市九年级学业水平考试模拟考数学试卷(解析版) 题型:解答题
如图,正方形纸片 的边长为4,将其沿
的边长为4,将其沿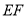 折叠,则图中①②③④四个三角形的周长之和为 .
折叠,则图中①②③④四个三角形的周长之和为 .

查看答案和解析>>
科目:初中数学 来源:2014-2015学年辽宁省东港市九年级九校联考数学试卷(解析版) 题型:选择题
下列说法不正确的是( )
A.一组邻边相等的矩形是正方形
B.对角线相等的菱形是正方形
C.对角线互相垂直的矩形是正方形
D.有一个角是直角的平行四边形是正方形
查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省盐城市盐都区西片九年级下学期第一次月考数学试卷(解析版) 题型:解答题
(本题满分10分)如图,在同一平面内,两条平行高速公路l1和l2间有一条“Z”型道路连通,其中AB段与高速公路l1成30°角,长为20km;BC段与AB、CD段都垂直,长为10km,CD段长为30km,求两高速公路间的距离(结果保留根号).

查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省联盟九年级下学期第一次月考数学试卷(解析版) 题型:填空题
有一组数据如下:3,a,4,6,7,它们的平均数是5,那么这组数据的方差是
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com