
【题目】如图,抛物线![]() 与y轴的交点为A,抛物线的顶点为
与y轴的交点为A,抛物线的顶点为![]() .
.

(1)求出抛物线的解析式;
(2)点P为x轴上一点,当△PAB的周长最小时,求出点P的坐标.
【答案】(1)y=![]() ;(2)
;(2) ![]()
【解析】
(1)已知A,B的坐标,运用待定系数法即可解答;
(2)先找A(0,-2)关于x轴的对称点为![]() (0,2),连接
(0,2),连接![]() B交x轴于点P,则此时△PAB的周长最小;然后再求出
B交x轴于点P,则此时△PAB的周长最小;然后再求出![]() P所在直线的解析式,然后令y=0,即可完成解答.
P所在直线的解析式,然后令y=0,即可完成解答.
解:(1)∵ 抛物线与y轴交于点A(0,-2),顶点为B(1,-3)
∴ 可设抛物线解析式![]() ,代入点A(0,-2)得a =1
,代入点A(0,-2)得a =1
∴抛物线解析式![]()
(2)设点A(0,-2)关于x轴的对称点为![]() (0,2),连接
(0,2),连接![]() B交x轴于点P,则此时△PAB的周长最小
B交x轴于点P,则此时△PAB的周长最小
设直线![]() B的解析式
B的解析式![]() ,代入点
,代入点![]() (0,2),B(1,-3)得:
(0,2),B(1,-3)得:![]()
解得:k=-5,b=2
∴ 直线![]() B的解析式
B的解析式![]()
当y=0时,![]()
∴ ![]()


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图(1),AB=CD,AD=BC,O为AC中点,过O点的直线分别与AD、BC相交于点M、N,那么∠1与∠2有什么关系?请说明理由;
若过O点的直线旋转至图(2)、(3)的情况,其余条件不变,那么图(1)中的∠1与∠2的关系成立吗?请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形纸片ABCD中,AB=4,AD=6,点P是边BC上的动点,现将纸片折叠,使点A与点P重合,折痕与矩形边的交点分别为E、F,要使折痕始终与边AB、AD有交点,则BP的取值范围是_________________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某自行车经销商计划投入7.1万元购进100辆A型和30辆B型自行车,其中B型车单价是A型车单价的6倍少60元.
(1)求A、B两种型号的自行车单价分别是多少元?
(2)后来由于该经销商资金紧张,投入购车的资金不超过5.86万元,但购进这批自行年的总数不变,那么至多能购进B型车多少辆?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某游客乘坐“金碧皇宫号游船”在长江和嘉陵江的交汇处A点,测得来福土最高楼顶点F的仰角为45°,此时他头项正上方146米的点B处有架航拍无人机测得来福士最高楼顶点F的仰角为31°,游船朝码头方向行驶120米到达码头C,沿坡度i=1:2的斜坡CD走到点D,再向前走160米到达来福士楼底E,则来福士最高楼EF的高度约为( )(结果精确到0.1,参考数据:sin31°≈0.52,cos31°≈0.87,tan31°≈0.60)
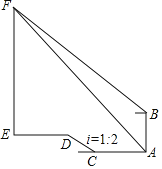
A.301.3米B.322.5米C.350.2米D.418.5米
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在初中阶段的函数学习中,我们经历了“确定函数的解析式利用函数图象研究其性质﹣运用函数解决问题”的学习过程.在画函数图象时,我们可以通过描点或平移或翻折等方法画出函数图象、下面我们対函数y=|![]() ﹣1|展开探索,请补充以下探索过程:
﹣1|展开探索,请补充以下探索过程:
(1)列表
x | … | ﹣1 | ﹣ | ﹣ | ﹣ | 0 |
|
|
| … |
|
|
| 2 |
|
|
| 3 | … | |
y | … |
|
|
|
| 2 |
| 3 | a | … | 3 | 1 |
| 0 |
|
| b |
| … | |
直接写出函数自变量x的取值范围,及a= ,b= ;
(2)在给出的平面直角坐标系中,请用你喜欢的方法画出这个函数的图象,并写出这个函数的一条性质: .
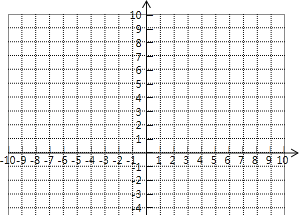
(3)若方程|![]() ﹣1|=m有且只有一个解,直接写出m的值: .
﹣1|=m有且只有一个解,直接写出m的值: .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com