
 上一个动点,且A(-1,0),E(1,0).
上一个动点,且A(-1,0),E(1,0).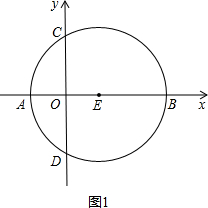
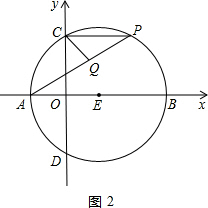
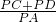 的值不变,②
的值不变,②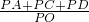 的值不变,其中有且只有一个是正确的,请你判断哪一个是正确的,并求其值.
的值不变,其中有且只有一个是正确的,请你判断哪一个是正确的,并求其值.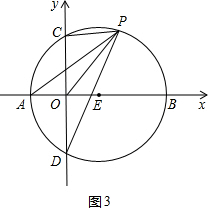
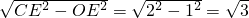 ,
,
 );
);
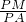 =
=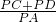 =
= .
.


科目:初中数学 来源: 题型:
| a-4 |
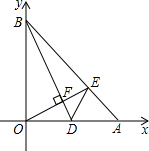 |4-b|=0
|4-b|=0查看答案和解析>>
科目:初中数学 来源: 题型:
 |
| BC |
| PC+PD |
| PA |
| PA+PC+PD |
| PO |
查看答案和解析>>
科目:初中数学 来源:2008-2009学年九年级数学元月调考模拟试卷(解析版) 题型:解答题
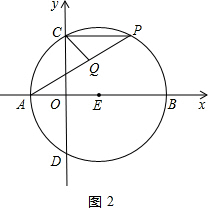
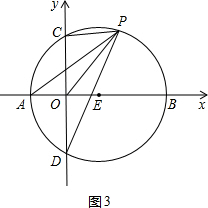
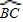 上一个动点,且A(-1,0),E(1,0).
上一个动点,且A(-1,0),E(1,0).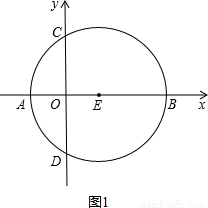
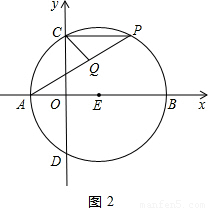
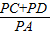 的值不变,②
的值不变,②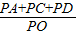 的值不变,其中有且只有一个是正确的,请你判断哪一个是正确的,并求其值.
的值不变,其中有且只有一个是正确的,请你判断哪一个是正确的,并求其值.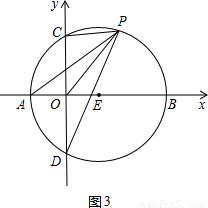
查看答案和解析>>
科目:初中数学 来源: 题型:
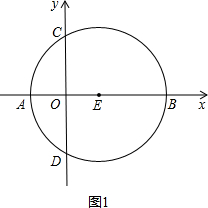
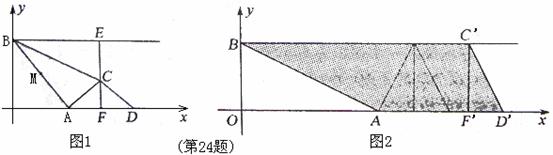
如图1,点A是![]() 轴正半轴上的动点,点B坐标为(0,4),M是线段AB的中点,将点M绕点A顺时针方向旋转90°得到点C,过点C作
轴正半轴上的动点,点B坐标为(0,4),M是线段AB的中点,将点M绕点A顺时针方向旋转90°得到点C,过点C作![]() 轴的垂线,垂足为F,过点B作
轴的垂线,垂足为F,过点B作![]() 轴的垂线与直线CF相交于点E,点D点A关于直线CF的对
轴的垂线与直线CF相交于点E,点D点A关于直线CF的对![]() 称点,连结AC,BC,CD,设点A的横坐标为
称点,连结AC,BC,CD,设点A的横坐标为![]()
(1)当![]() 时,求CF的长;
时,求CF的长;
(2)①当![]() 为何值时,点C落在线段BD上?
为何值时,点C落在线段BD上?
②设△BCE的面积为S,求S与![]() 之间的函数关系式;
之间的函数关系式;
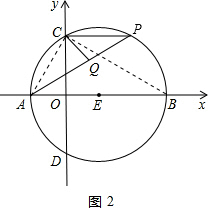
(3)如图2,当![]() 点C与点E重合时,△CDF沿
点C与点E重合时,△CDF沿![]() 轴左右平移得到△C’D
轴左右平移得到△C’D![]() ’F’,再将A,B,C’,D’为顶点的四边形沿C’F’剪开,得到两个图形,用这两个图形拼成不重叠且无缝隙的图形恰好是三角形,请直接写出所有符合上述条件的点C’的坐标。
’F’,再将A,B,C’,D’为顶点的四边形沿C’F’剪开,得到两个图形,用这两个图形拼成不重叠且无缝隙的图形恰好是三角形,请直接写出所有符合上述条件的点C’的坐标。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com