
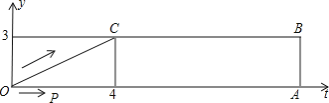
【题目】如图,梯形OABC中,O为直角坐标系的原点,A、B、C的坐标分别为(14,0)、(14,3)、(4,3).点P、Q同时从原点出发,分别作匀速运动,其中点P沿OA向终点A运动,速度为每秒1个单位;点Q沿OC、CB向终点B运动,当这两点中有一点到达自己的终点时,另一点也停止运动.设P从出发起运动了t秒.
(1)如果点Q的速度为每秒2个单位,①试分别写出这时点Q在OC上或在CB上时的坐标(用含t的代数式表示,不要求写出t的取值范围);
②求t为何值时,PQ∥OC?
(2)如果点P与点Q所经过的路程之和恰好为梯形OABC的周长的一半,①试用含t的代数式表示这时点Q所经过的路程和它的速度;
②试问:这时直线PQ是否可能同时把梯形OABC的面积也分成相等的两部分?如有可能,求出相应的t的值和P、Q的坐标;如不可能,请说明理由.
【答案】(1)①点Q在OC上时Q(![]() t,
t,![]() t),点Q在CB上时Q(2t﹣1,3);②t=5;(2)①v=
t),点Q在CB上时Q(2t﹣1,3);②t=5;(2)①v=![]() ,点Q所经过的路程为(16﹣t);②直线PQ不可能同时把梯形OABC的面积也分成相等的两部分.
,点Q所经过的路程为(16﹣t);②直线PQ不可能同时把梯形OABC的面积也分成相等的两部分.
【解析】
试题分析:(1)①根据相似三角形的性质即可求得点Q在OC上时的坐标;根据路程即可求得点Q在CB上时的横坐标是(2t﹣5),纵坐标和点C的纵坐标一致,是3;
②显然此时Q在CB上,由平行四边形的知识可得,只需根据OP=CQ列方程求解;
(2)①设Q的速度为v,根据P与点Q所经过的路程之和恰好为梯形OABC的周长的一半,即可建立函数关系式;
②显然Q应在CB上,根据面积和①中的结论得到关于t的方程,进行求解.
试题解析:(1)①点Q在OC上时Q(![]() t,
t,![]() t),点Q在CB上时Q(2t﹣1,3).
t),点Q在CB上时Q(2t﹣1,3).
②显然Q在CB上,由平行四边形的知识可得,只须OP=CQ.所以2t﹣5=t得t=5.
(2)①设Q的速度为v,先求梯形的周长为32,可得t+vt=16,所以v=![]() ,点Q所经过的路程为(16﹣t);
,点Q所经过的路程为(16﹣t);
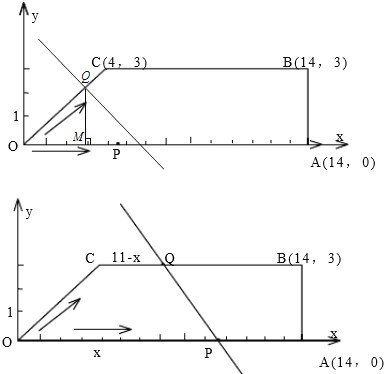
②当Q在OC上时,做QM⊥OA,垂足为M,则QM=(16﹣t)×![]() ,∴S△OPQ=
,∴S△OPQ=![]() ×
×![]() (16﹣t)t=
(16﹣t)t=![]() t(16﹣t)=
t(16﹣t)=![]() S梯形OABC,则令
S梯形OABC,则令![]() t(16﹣t)=18,解得t1=10,t2=6,当t1=10时,16﹣x=6,此时点Q不在OC上,舍去;当t2=6时,16﹣x=10,此时点Q也不在OC上,舍去;∴当Q点在OC上时,PQ不可能同时把梯形OABC的面积也分成相等的两部分.
t(16﹣t)=18,解得t1=10,t2=6,当t1=10时,16﹣x=6,此时点Q不在OC上,舍去;当t2=6时,16﹣x=10,此时点Q也不在OC上,舍去;∴当Q点在OC上时,PQ不可能同时把梯形OABC的面积也分成相等的两部分.
当Q点在CB上时,CQ=16﹣t﹣5=11﹣x,∴S梯形OPQC=![]() ×(11﹣x+x)×3=
×(11﹣x+x)×3=![]() ≠18,∴当Q点在CB上时,PQ不可能同时把梯形OABC的面积也分成相等的两部分.
≠18,∴当Q点在CB上时,PQ不可能同时把梯形OABC的面积也分成相等的两部分.
综上所述,直线PQ不可能同时把梯形OABC的面积也分成相等的两部分.


科目:初中数学 来源: 题型:
【题目】对于二次函数y=﹣2x2,下列结论正确的是( )
A.y随x的增大而增大B.图象关于直线x=0对称
C.图象开口向上D.无论x取何值,y的值总是负数
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,AC=8,AB=10,△ABC的面积为30,AD平分∠BAC,F、E分别为AC、AD上两动点,连接CE、EF,则CE+EF的最小值为 . 
查看答案和解析>>
科目:初中数学 来源: 题型:
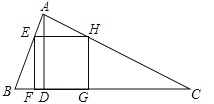
【题目】如图,△ABC为锐角三角形,AD是BC边上的高,正方形EFGH的一边FG在BC上,顶点E、H分别在AB、AC上,已知BC=40cm,AD=30cm.
(1)求证:△AEH∽△ABC;
(2)求这个正方形的边长与面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】李明到离家2.1千米的学校参加初三联欢会,到学校时发现演出道具还放在家中,此时距联欢会开始还有42分钟,于是他立即匀速步行回家,在家拿道具用了1分钟,然后立即匀速骑自行车返回学校.已知李明骑自行车到学校比他从学校步行到家用时少20分钟,且骑自行车的速度是步行速度的3倍.
(1)李明步行的速度(单位:米/分)是多少?
(2)李明能否在联欢会开始前赶到学校?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知A(0,2),B(4,0).
(1)如图1,连接AB,若D(0,﹣6),DE⊥AB于点E,B、C关于y轴对称,M是线段DE上的一点,且DM=AB,连接AM,试判断线段AC与AM之间的位置和数量关系,并证明你的结论;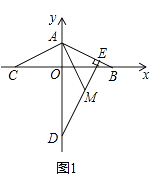
(2)如图2,在(1)的条件下,若N是线段DM上的一个动点,P是MA延长线上的一点,且DN=AP,连接PN交y轴于点Q,过点N作NH⊥y轴于点H,当N点在线段DM上运动时,△MQH的面积是否为定值?若是,请求出这个值;若不是,请说明理由.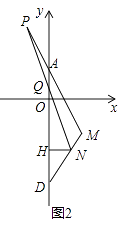
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,锐角三角形ABC中(AB>AC),AH⊥BC,垂足为H,E、D、F分别是各边的中点,则四边形EDHF是( ) 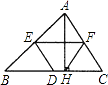
A.梯形
B.等腰梯形
C.直角梯形
D.矩形
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com