
【题目】如图,正方形ABCD的边长是18,点E是AB边上的一个动点,点F是CD边上一点,![]() ,连接EF,把正方形ABCD沿EF折叠,使点A,D分别落在点
,连接EF,把正方形ABCD沿EF折叠,使点A,D分别落在点![]() ,
,![]() 处,当点
处,当点![]() 落在直线BC上时,线段AE的长为________.
落在直线BC上时,线段AE的长为________.

【答案】4或16
【解析】
分两种情况:①D′落在线段BC上,②D′落在线段BC延长线上,分别连接ED、ED′、DD′,利用折叠的性质以及勾股定理,即可得到线段AE的长.
解:分两种情况:
①当D′落在线段BC上时,连接ED、ED′、DD′,如图1所示:
由折叠可得,D,D'关于EF对称,即EF垂直平分DD',
∴DE=D′E,
∵正方形ABCD的边长是18,
∴AB=BC=CD=AD=18,
∵CF=8,
∴DF=D′F=CDCF=10,
∴CD′=![]() =6,
=6,
∴BD'=BCCD'=12,
设AE=x,则BE=18x,
在Rt△AED和Rt△BED'中,
由勾股定理得:DE2=AD2+AE2=182+x2,D'E2=BE2+BD'2=(18x)2+122,
∴182+x2=(18x)2+122,
解得:x=4,即AE=4;
②当D′落在线段BC延长线上时,连接ED、ED′、DD′,如图2所示:
由折叠可得,D,D'关于EF对称,即EF垂直平分DD',
∴DE=D′E,
∵正方形ABCD的边长是18,
∴AB=BC=CD=AD=18,
∵CF=8,
∴DF=D′F=CDCF=10,CD'=![]() =6,
=6,
∴BD'=BC+CD'=24,
设AE=x,则BE=18x,
在Rt△AED和Rt△BED'中,
由勾股定理得:DE2=AD2+AE2=182+x2,D'E2=BE2+BD'2=(18x)2+242,
∴182+x2=(18x)2+242,
解得:x=16,即AE=16;
综上所述,线段AE的长为4或16;
故答案为:4或16.



科目:初中数学 来源: 题型:
【题目】如图,Rt△OAB的顶点O与坐标原点重合,∠AOB=90°,AO=2BO,当点A在反比例函数![]() (x>0)的图像上移动时,点B的坐标满足的函数表达式为( )
(x>0)的图像上移动时,点B的坐标满足的函数表达式为( )

A. ![]() (x<0) B.
(x<0) B. ![]() (x<0)
(x<0)
C. ![]() (x<0) D.
(x<0) D. ![]() (x<0)
(x<0)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】以下是两张不同类型火车的车票:(“D×××次”表示动车,“G×××次”表示高铁):
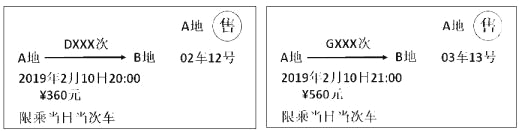
(1)根据车票中的信息填空:两车行驶方向 ,出发时刻 (填“相同”或“不同”);
(2)已知该动车和高铁的平均速度分别为200km/h,300km/h,如果两车均按车票信息准时出发,且同时到达终点,求A,B两地之间的距离;
(3)在(2)的条件下,请求出在什么时刻两车相距100km?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】高空抛物极其危险,是我们必须杜绝的行为.据研究,高空抛物下落的时间t(单位:s)和高度 h(单位:m)近似满足公式 t=![]() (不考虑风速的影响)
(不考虑风速的影响)
(1)从 50m 高空抛物到落地所需时间 t1 是多少 s,从 100m 高空抛物到落地所 需时间 t2 是多少 s;
(2)t2 是 t1 的多少倍?
(3)经过 1.5s,高空抛物下落的高度是多少?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】台湾是中国领土不可分割的一部分,两岸在政治、经济、文化等领域交流越来越深,在北京故宫博物院成立90周年院庆时,两岸故宫同根同源,合作举办了多项纪念活动.据统计,北京故宫博物院与台北故宫博物院现共有藏品约245万件,其中台北故宫博物院藏品数量比北京故宫博物院藏品数量的![]() 还少25万件,求北京故宫博物院约有多少万件藏品?
还少25万件,求北京故宫博物院约有多少万件藏品?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图(1), 点![]() 为直线
为直线![]() 上一点,过点
上一点,过点![]() 作射线
作射线![]() , 将一直角的直角项点放在点
, 将一直角的直角项点放在点![]() 处,即
处,即![]() 反向延长射线
反向延长射线![]() ,得到射线
,得到射线![]() .
.
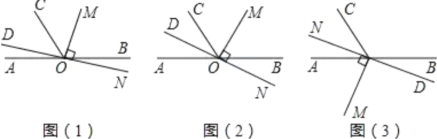
(1)当![]() 的位置如图(1)所示时,使
的位置如图(1)所示时,使![]() ,若
,若![]() ,求
,求![]() 的度数.
的度数.
(2)当![]() 的位置如图(2)所示时,使一边
的位置如图(2)所示时,使一边![]() 在
在![]() 的内部,且恰好平分
的内部,且恰好平分![]() ,
,
问:射线![]() 的反向延长线
的反向延长线![]() 是否平分
是否平分![]() 请说明理由:注意:不能用问题
请说明理由:注意:不能用问题![]() 中的条件
中的条件
(3)当![]() 的位置如图
的位置如图![]() 所示时,射线
所示时,射线![]() 在
在![]() 的内部,若
的内部,若![]() .试探究
.试探究![]() 与
与![]() 之间的数量关系,不需要证明,直接写出结论.
之间的数量关系,不需要证明,直接写出结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知![]() 三点在数轴上所对应的数分别为
三点在数轴上所对应的数分别为![]() 且
且![]() 满足
满足![]() .动点
.动点![]() 从点
从点![]() 出发,以2单位/秒的速度向右运动,同时,动点
出发,以2单位/秒的速度向右运动,同时,动点![]() 从点
从点![]() 出发,以1单位秒的速度向左运动,线段
出发,以1单位秒的速度向左运动,线段![]() 为“变速区”,规则为: 从点
为“变速区”,规则为: 从点![]() 运动到点
运动到点![]() 期间速度变为原来的一半,之后立刻恢复原速,从点
期间速度变为原来的一半,之后立刻恢复原速,从点![]() 运动到点
运动到点![]() 期间速度变为原来的两倍,之后也立刻恢复原速.当点
期间速度变为原来的两倍,之后也立刻恢复原速.当点![]() 到达点
到达点![]() 时,两点都停止运动.设运动的时间为
时,两点都停止运动.设运动的时间为![]() 秒.
秒.
(1) ![]() ______,
______,![]() ______,
______,![]() ______;
______;
(2)①动点![]() 从点
从点![]() 运动至点
运动至点![]() 时,求
时,求![]() 的值;
的值;
②![]() 两点相遇时,求相遇点在数轴上所对应的数;
两点相遇时,求相遇点在数轴上所对应的数;
(3)若点![]() 为线段
为线段![]() 中点,当
中点,当![]() ________秒时,
________秒时,![]() .
.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,函数![]() 和
和![]() 的图象分别为直线
的图象分别为直线![]() ,
,![]() ,过点
,过点![]() 作
作![]() 轴的垂线交
轴的垂线交![]() 于点
于点![]() ,过
,过![]() 点作
点作![]() 轴的垂线交
轴的垂线交![]() 于点
于点![]() ,过点
,过点![]() 作
作![]() 轴的垂线交
轴的垂线交![]() 于点
于点![]() ,过点
,过点![]() 作
作![]() 轴的垂线交
轴的垂线交![]() 于点
于点![]() ,…,依次进行下去,则点
,…,依次进行下去,则点![]() 的坐标为______,点
的坐标为______,点![]() 的坐标为______.
的坐标为______.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,数轴上点![]() 分别对应数
分别对应数![]() ,其中
,其中![]() .
.

![]() 当
当![]() 时,线段
时,线段![]() 的中点对应的数是_ _____ .(直接填结果)
的中点对应的数是_ _____ .(直接填结果)
![]() 若该数轴上另有一点
若该数轴上另有一点![]() 对应着数
对应着数![]() .
.
①当![]() ,且
,且![]() 时,求代数式
时,求代数式![]() 的值:
的值:
②![]() .且
.且![]() 时学生小朋通过演算发现代数式
时学生小朋通过演算发现代数式![]() 是一个定值
是一个定值
老师点评:小朋同学的演算发现还不完整!
请你通过演算解释为什么“小朋的演算发现”是不完整的?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com