
【题目】如图,在△ABC中,AB=AC,点D是BC的中点,点E是△ABC内一点,若∠AEB=∠CED=90°,AE=BE,CE=DE=2,则图中阴影部分的面积等于__________.

科目:初中数学 来源: 题型:
【题目】探究活动有一圆柱形食品盒,它的高等于8cm,底面直径为![]() cm,蚂蚁爬行的速度为2cm/s
cm,蚂蚁爬行的速度为2cm/s
(1)如果在盒内下底面的A处有一只蚂蚁,它想吃到盒内对面中部点B处的食物,那么它至少需要多少时间?(盒的厚度和蚂蚁的大小忽略不计,结果可含根号)

(2)如果在盒外下底面的A处有一只蚂蚁,它想吃到盒内对面中部点B处的食物,那么它至少需要多少时间?(盒的厚度和蚂蚁的大小忽略不计)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图△ABC中,∠ABC与∠ACB的平分线交于点F,过点F作DE∥BC交AB于点D交AC于点E,那么下列结论中正确的是 ( )
①△BDF和△CEF都是等腰三角形
②DE=BD+CE
③△ADE的周长等于AB和AC的和
④BF=CF

A. ①②③④ B. ①②③ C. ①② D. ①
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,菱形OABC的顶点O在坐标原点,顶点A在x轴上,∠B=120°,OA=2,将菱形OABC绕原点顺时针旋转105°至OA′B′C′的位置,则点B′的坐标为( ) 
A.( ![]() ,﹣
,﹣ ![]() )
)
B.(﹣ ![]() ,
, ![]() )
)
C.(2,﹣2)
D.( ![]() ,﹣
,﹣ ![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知一次函数![]() ,
,![]() 随
随![]() 增大而增大,它的图象经过点
增大而增大,它的图象经过点![]() 且与
且与![]() 轴的夹角为
轴的夹角为![]() ,
,
![]() 确定这个一次函数的解析式;
确定这个一次函数的解析式;
![]() 假设已知中的一次函数的图象沿
假设已知中的一次函数的图象沿![]() 轴平移两个单位,求平移以后的直线及直线与
轴平移两个单位,求平移以后的直线及直线与![]() 轴的交点坐标.
轴的交点坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列方程,是一元二次方程的是( )
①3x2+x=20,②2x2﹣3xy+4=0,③x2 ![]() =4,④x2=0,⑤x2﹣3x﹣4=0.
=4,④x2=0,⑤x2﹣3x﹣4=0.
A.①②
B.①②④⑤
C.①③④
D.①④⑤
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若关于x的一元二次方程(k﹣1)x2+2x﹣2=0有不相等实数根,则k的取值范围是( )
A.k> ![]()
B.k≥ ![]()
C.k> ![]() 且k≠1
且k≠1
D.k≥ ![]() 且k≠1
且k≠1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知在△ABC,△ADE中,∠BAC=∠DAE=90°,AB=AC,AD=AE,点C,D,E三点在同一条直线上,连接BD,BE.以下四个结论:
①BD=CE;②∠ACE+∠DBC=45°;③BD⊥CE;④∠BAE+∠DAC=180°.其中结论正确的个数是( )
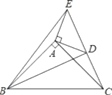
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数y=ax2+bx+c的图象如图所示,对称轴x=﹣1,下列五个代数式ab、ac、a﹣b+c、b2﹣4ac、2a+b中,值大于0的个数为( ) 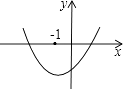
A.5
B.4
C.3
D.2
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com