
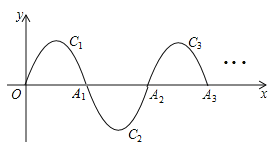
【题目】如图,一段抛物线:y=-x(x-2)(0≤x≤2)记为C1,它与x轴交于两点O、A1;将C1绕A1旋转180°得到C2 ,交x轴于A2;将C2绕A2旋转180°得到C3 ,交x轴于A3;…如此进行下去,直至得到C1010.若点P(2019,m)在第1010段抛物线C1010上,则m=_____________.
【答案】-1
【解析】
根据在旋转过程中抛物线开口大小不变,结合交点坐标可得抛物线表达式的变化规律,由此可得抛物线C1010的解析式,由P(2019,m)在抛物线C1010上即可求得m值.
解:∵一段抛物线C1:y=-x(x-2)(0≤x≤2),
∴图象C1与x轴交点坐标为:(0,0),(2,0),
∵将C1绕点A1旋转180°得C2,交x轴于点A2;,
∴抛物线C2:y=(x-2)(x-4)(2≤x≤4),
∵将C2绕点A1旋转180°得C3,交x轴于点A3;,
∴抛物线C3:y=-(x-4)(x-6)(2≤x≤4),
…..
∴抛物线Cn:![]() ,
,
∴抛物线C1010:![]() ,
,
∵点P(2019,m)在第1010段抛物线C1010上,
∴![]() .
.
故答案为:-1.


科目:初中数学 来源: 题型:
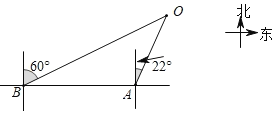
【题目】2019年4月23日是中国人民解放军海军成立70周年纪念日,届时将在青岛举行盛大的多国海军庆祝活动.为此我国海军进行了多次军事演习.如图,在某次军事演习时,舰艇A发现在他北偏东22°方向上有不明敌舰在指挥中心O附近徘徊,快速报告给指挥中心,此时在舰艇A正西方向50海里处的舰艇B接到返回指挥中心的行动指令,舰艇B迅速赶往在他北偏东60°方向的指挥中心处,舰艇B的速度是80海里/小时,请根据以上信息,求舰艇B到达指挥中心O的时间.(结果精确到0.1小时,参考数据:(sin22°≈0.37,cos22°≈0.93,tan22°≈0.40,![]() =1.73)
=1.73)
查看答案和解析>>
科目:初中数学 来源: 题型:
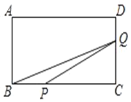
【题目】如图,已知矩形ABCD中,AB=4cm,BC=8cm.动点P在边BC上从点B向C运动,速度为1cm/s;同时动点Q从点C出发,沿折线C→D→A运动,速度为2cm/s.当一个点到达终点时,另一个点随之停止运动。设点P运动的时间为t(s),△BPQ的面积为S(cm2),则描述S(cm2)与时间t(s)的函数关系的图象大致是( )
A.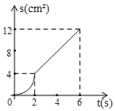 B.
B.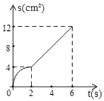
C.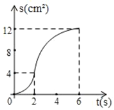 D.
D.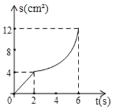
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在Rt△ABC中,∠ACB=90°,tan∠BAC=![]() . 点D在边AC上(不与A,C重合),连结BD,F为BD中点.
. 点D在边AC上(不与A,C重合),连结BD,F为BD中点.
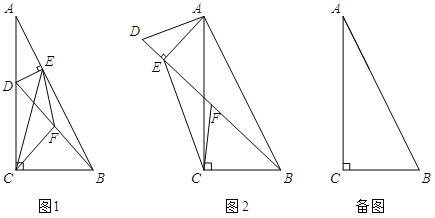
(1)若过点D作DE⊥AB于E,连结CF、EF、CE,如图1.设![]() ,则k= ;
,则k= ;
(2)若将图1中的△ADE绕点A旋转,使得D、E、B三点共线,点F仍为BD中点,如图2所示.求证:BE-DE=2CF;
(3)若BC=6,点D在边AC的三等分点处,将线段AD绕点A旋转,点F始终为BD中点,求线段CF长度的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+bx+c(a≠0)的图象过点C(0,1),顶点为Q(2,3),点D在x轴正半轴上,且OD=OC.
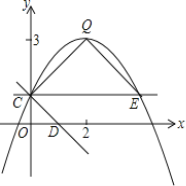
(1)求直线CD的解析式;
(2)求抛物线的解析式;
(3)将直线CD绕点C逆时针方向旋转45°所得直线与抛物线相交于另一点E,求证:△CEQ∽△CDO;
(4)在(3)的条件下,若点P是线段QE上的动点,点F是线段OD上的动点,问:在P点和F点移动过程中,△PCF的周长是否存在最小值?若存在,求出这个最小值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
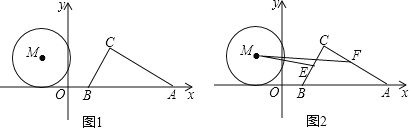
【题目】如图1,有一块直角三角板,其中![]() ,
,![]() ,
,![]() ,A、B在x轴上,点A的坐标为
,A、B在x轴上,点A的坐标为![]() ,圆M的半径为
,圆M的半径为![]() ,圆心M的坐标为
,圆心M的坐标为![]() ,圆M以每秒1个单位长度的速度沿x轴向右做平移运动,运动时间为t秒;
,圆M以每秒1个单位长度的速度沿x轴向右做平移运动,运动时间为t秒;
![]() 求点C的坐标;
求点C的坐标;
![]() 当点M在
当点M在![]() 的内部且
的内部且![]() 与直线BC相切时,求t的值;
与直线BC相切时,求t的值;
![]() 如图2,点E、F分别是BC、AC的中点,连接EM、FM,在运动过程中,是否存在某一时刻,使
如图2,点E、F分别是BC、AC的中点,连接EM、FM,在运动过程中,是否存在某一时刻,使![]() ?若存在,直接写出t的值,若不存在,请说明理由.
?若存在,直接写出t的值,若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com