先观察:1-$\frac{1}{{2}^{2}}$=$\frac{1}{2}$×$\frac{3}{2}$.1-$\frac{1}{{3}^{2}}$=$\frac{2}{3}$×$\frac{4}{3}$.1-$\frac{1}{{4}^{2}}$=$\frac{3}{4}$×$\frac{5}{4}$.-(1)探究规律填空:1-$\frac{1}{{n}^{2}}$=$\frac{n-1 题目和参考答案——青夏教育精英家教网—

精英家教网 > 初中数学 > 题目详情

13．先观察：1-$\frac{1}{{2}^{2}}$=$\frac{1}{2}$×$\frac{3}{2}$，1-$\frac{1}{{3}^{2}}$=$\frac{2}{3}$×$\frac{4}{3}$，1-$\frac{1}{{4}^{2}}$=$\frac{3}{4}$×$\frac{5}{4}$，…
（1）探究规律填空：1-$\frac{1}{{n}^{2}}$=$\frac{n-1}{n}$×$\frac{n+1}{n}$；
（2）计算：（1-$\frac{1}{{2}^{2}}$）•（1-$\frac{1}{{3}^{2}}$）•（1-$\frac{1}{{4}^{2}}$）…（1-$\frac{1}{201{5}^{2}}$）

分析（1）利用平方差公式变形即可得到结果；
（2）原式利用平方差公式化简，计算即可得到结果．

解答解：（1）原式=$\frac{n-1}{n}$×$\frac{n+1}{n}$；
（2）原式=（1-$\frac{1}{2}$）（1+$\frac{1}{2}$）（1-$\frac{1}{3}$）（1+$\frac{1}{3}$）…（1-$\frac{1}{2015}$）（1+$\frac{1}{2015}$）
=$\frac{1}{2}$×$\frac{3}{2}$×$\frac{2}{3}$×$\frac{4}{3}$×…×$\frac{2014}{2015}$×$\frac{2016}{2015}$
=$\frac{1008}{2015}$，
故答案为：（1）$\frac{n-1}{n}$；$\frac{n+1}{n}$

点评此题考查了有理数的混合运算，熟练掌握平方差公式是解本题的关键．

练习册系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：初中数学 来源： 题型：填空题

2．

已知等边△ABC中，点D，E分别在边AB，BC上，把△BDE沿直线DE翻折，使点B落在点B′处，DB′，EB′分别交边AC于点F，G，若∠ADF=60°，则∠EGC的度数为60°．

查看答案和解析>>

科目：初中数学 来源： 题型：解答题

3．某学校组织了一次“五城联创”知识竞赛活动，根据初赛成绩分别从三个年级中选出了10名同学参加决赛，成绩统计如下：

	决赛成绩（单位：分）
七年级	82　86　88　81　88　97　80　74　90　89
八年级	85　88　87　97　85　76　88　80　86　88
九年级	81　83　79　79　79　92　99　88　89　86

（1）补全下面的表格：

年纪	平均数	众数	中位数
七年级	85.5	88	87
八年级	86	88	86.5
九年级	85.5	79	84.5

（2）从以下两个方面对三个年纪的成绩进行评价：
①从平均数和众数方面分析，八年级成绩较好；
②从中位数和众数方面分析，七年级成绩较好；
（3）学校决定根据决赛成绩，从某个年级中选出3人参加总决赛，你认为该选取哪个年纪的学生参赛？并写出理由．

查看答案和解析>>

科目：初中数学 来源： 题型：填空题

1．阅读：（x-1）（x+1）=x²-1，（x-1）（x²+x+1）=x³-1，（x-1）（x³+x²+x+1）=x⁴-1．
由上面的规律得（x-1）（xⁿ+x^n-1+…+x+1）=xⁿ⁺¹-1（n为正整数）；
根据这一规律进行计算：2²⁰¹⁴-2²⁰¹³+2²⁰¹²-2²⁰¹¹+2²⁰¹⁰…-2³+2²-2+1=$\frac{{2}^{2015}+1}{3}$．

查看答案和解析>>

科目：初中数学 来源： 题型：填空题

8．

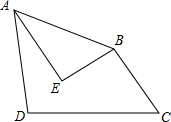如图，在四边形ABCD中，AB=AD，∠BAD=∠C=60°，点E为四边形ABCD内部一点，连接AE、BE，∠AEB=∠CBE=90°，BC=3，则线段BE的长为$\frac{3\sqrt{3}}{2}$．