
 如图,大正方形的边长为a,小正方形的边长为b.
如图,大正方形的边长为a,小正方形的边长为b.分析 (1)根据题意和图形可知阴影部分的面积是大正方形的面积加上小正方形的面积再减去△AGF和△ACD的面积,然后用相应的代数式表示出来即可解答本题;
(2)将(1)中S的代数式变形,然后将a+b=4,ab=2,代入即可解答本题.
解答 解:(1)由图可得,
阴影部分的面积S是:${a}^{2}+{b}^{2}-\frac{{a}^{2}}{2}-\frac{(a+b)b}{2}$=$\frac{{a}^{2}}{2}+\frac{{b}^{2}}{2}-\frac{ab}{2}$,
即阴影部分的面积S是$\frac{{a}^{2}}{2}+\frac{{b}^{2}}{2}-\frac{ab}{2}$;
(2)∵a+b=4,ab=2,
∴S=$\frac{{a}^{2}}{2}+\frac{{b}^{2}}{2}-\frac{ab}{2}$=$\frac{{a}^{2}+{b}^{2}}{2}-\frac{ab}{2}$=$\frac{(a+b)^{2}-2ab}{2}-\frac{ab}{2}$=$\frac{{4}^{2}-2×2}{2}-\frac{2}{2}$=5,
即如果a+b=4,ab=2,S的值是5.
点评 本题考查整式的混合运算、代数式求值,解题的关键是明确题意,用相应的代数式表示出阴影部分的面积,会求代数式的值.


 长江作业本同步练习册系列答案
长江作业本同步练习册系列答案科目:初中数学 来源: 题型:解答题
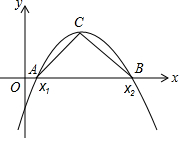 如图,抛物线y=(1-m)x2+4x-3的开口向下,与x轴交于A(x1,0),B(x2,0)两点,其中x1≤x2
如图,抛物线y=(1-m)x2+4x-3的开口向下,与x轴交于A(x1,0),B(x2,0)两点,其中x1≤x2查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 4 | B. | $2\sqrt{5}$ | C. | $\frac{{18\sqrt{3}}}{13}$ | D. | $\frac{{12\sqrt{3}}}{13}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
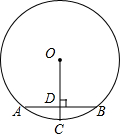 如图,AB为⊙O的弦,AB=6cm,OC⊥AB于D,交⊙O于点C,且CD=1cm,则⊙O的半径为( )
如图,AB为⊙O的弦,AB=6cm,OC⊥AB于D,交⊙O于点C,且CD=1cm,则⊙O的半径为( )| A. | 5cm | B. | 6cm | C. | 8cm | D. | 10cm |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,C为射线AB上一点,AB=30,AC比BC的$\frac{1}{4}$多5,P,Q两点分别从A,B两点同时出发.分别以2单位/秒和1单位/秒的速度在射线AB上沿AB方向运动,运动时间为t秒,M为BP的中点,N为QM的中点,以下结论:
如图,C为射线AB上一点,AB=30,AC比BC的$\frac{1}{4}$多5,P,Q两点分别从A,B两点同时出发.分别以2单位/秒和1单位/秒的速度在射线AB上沿AB方向运动,运动时间为t秒,M为BP的中点,N为QM的中点,以下结论:| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com