
��ͼ����֪������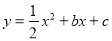 ��x�ύ��A��B���㣬�Գ���Ϊֱ��
��x�ύ��A��B���㣬�Գ���Ϊֱ��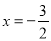 ��ֱ��AD���������ڵ�D��2��3����
��ֱ��AD���������ڵ�D��2��3����
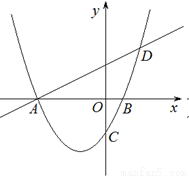
��1���������ߵĽ���ʽ��
��2����֪��MΪ�����������������ϵ�һ���㣬����M��ʲôλ��ʱ�ı���AMCO��������������ֵ��
��3�����ı���AMCO������ʱ������M��ֱ��ƽ����y�ᣬ������ֱ�����Ƿ����һ����Q��ΪԲ�ģ�OQΪ�뾶����ֱ��BC���е�Բ�������ڣ����Բ��Q�����ꣻ�������ڣ���˵�����ɣ�
��1�������ߵĽ���ʽΪ .��
.��
(2) ����MΪ(��2����3)ʱ�ı���AMCO��������ֵ�����ֵΪ8��
(3) ����һ����Q��ΪԲ�ģ�OQΪ�뾶����ֱ��BC���е�Բ����Q������Ϊ����2��4����2����1��������
��������
�����������1���ɴ���ϵ�������ɵã�
��2������OM�����ı���AMCO�ɷ�Ϊ���������Σ���M������꣬��ɱ�ʾ�����������ε�����������ɵõ���������ֵ
��3�������ȼ�����������ĵ㣬Ȼ��������е��������м��㼴��
�����������1����������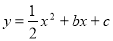 �ĶԳ�����ֱ��
�ĶԳ�����ֱ��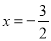 ,
,
�� �����
�����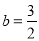 .
.
��������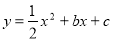 ����D(2,3),
����D(2,3),
��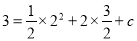 �����
�����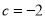 .
.
�������ߵĽ���ʽΪ .
.
��2�������ߵĽ���ʽΪ��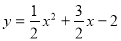 ,
,
��x��0����y����2����C��0�� -2����
��y��0����x����4��1����A(-4��0)��B��1��0����
���M����Ϊ(m��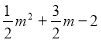 )������MO��
)������MO��
��S�ı���AMCO��S��AMO��S��CMO
��
��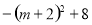
�൱m����2ʱ��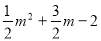 ����3
����3
�൱��MΪ(��2����3)ʱ�ı���AMCO��������ֵ�����ֵΪ8������
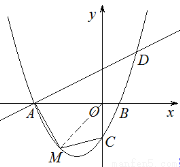
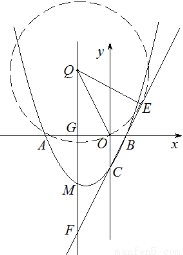
��3��������������ġ�Q��
��ֱ��x����2��x�ύ�ڵ�G����ֱ��BC���ڵ�F����ֱ��BC�Ľ���ʽΪy��kx��b��
��B��1��0����C��0����2������ã�
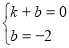 ����ã�k��2��b����2��
����ã�k��2��b����2��
��ֱ��BC����ʽΪ��y��2x��2��
��x����2����y����6����F����2����6����GF��6��
��Rt��BGF�У��ɹ��ɶ����ã�
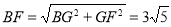 ,
,
��Q����2��n��������Rt��QGO�У��ɹ��ɶ����ã�
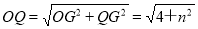 .
.
���Q��ֱ��BC�����ڵ�E����QE��OQ��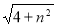 ��
��
��Rt��BGF��Rt��QEF��
�ߡ�BGF����QEF��90�㣬��BFG����QFE��
��Rt��BGF��Rt��QEF.
�� ����
���� .
.
����ã�n2��3n��4��0�����n��4��n����1��
�����һ����Q��ΪԲ�ģ�OQΪ�뾶����ֱ��BC���е�Բ����Q������Ϊ����2��4����2����1����
���㣺1������ϵ������2�����κ��������ʣ�3�����ɶ�����4�����ߵ�����


 ���Ǽ���С����ϵ�д�
���Ǽ���С����ϵ�д� �Ͻ�ƽ���Ȿϵ�д�
�Ͻ�ƽ���Ȿϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ��2013-2014ѧ�����ɹž��꼶6���п�ģ����ѧ�Ծ��������棩 ���ͣ������
ij��ѧ���꼶��ѧ��ȤС��Ϊ����У����˸߶ȣ���ͼ����C������˶���A������Ϊ30������ǰ����6����D�㣬��D������˶���A������Ϊ60��(������ĸ߶Ȳ���).
��1��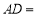 �ף�
�ף�
��2�������AB�ĸ߶ȣ��������1λС����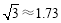 ��.
��.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2013-2014ѧ�����ɹź��ױ����о��꼶���Ĵ��¿���ѧ�Ծ��������棩 ���ͣ�ѡ����
����Բ���У��뾶�ֱ�Ϊ4��7�������ǵ�Բ�ľ����� ��
A��2 B��3 C��6 D��11
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2013-2014ѧ������ʡ��Ϫ��ҵˮƽģ�⿼����ѧ�Ծ��������棩 ���ͣ������
��x= ʱ����ʽ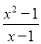 ��ֵΪ��.
��ֵΪ��.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2013-2014ѧ������ʡ��Ϫ��ҵˮƽģ�⿼����ѧ�Ծ��������棩 ���ͣ�ѡ����
�Ѳ���ʽ�� �Ľ⼯��ʾ�������ϣ���ȷ����
�Ľ⼯��ʾ�������ϣ���ȷ����

A B C D
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2013-2014ѧ������ʡ��Ϫ��ҵˮƽ��ϰ������ѧ�Ծ��������棩 ���ͣ������
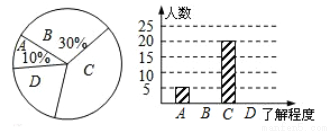
2014��3��20�գ�����ʦ�ͱ���ѧ���ԡ������¼������˽�̶Ƚ�����һ�ε���ͳ�ƣ���ͼ�����ɼ����ݺ���Ƶ�������������ͳ��ͼ��A�����˽⣬B��һ���˽⣬C���˽�϶࣬D����Ϥ�����������ͼ���ṩ����Ϣ����������⣺
��1����ð�ж�����ѧ����
��2��������ͳ��ͼ�У�����ʾ��һ���˽⡱�IJ��ֲ���������
��3��������ͳ��ͼ�У���������˽�϶ࡱ��������Ӧ��Բ�ĽǵĶ�����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2013-2014ѧ������ʡ��Ϫ��ҵˮƽ��ϰ������ѧ�Ծ��������棩 ���ͣ������
С�����ˮ�����ˮ�绰���ɵ绰��������һ�����ּDz����ˣ�ֻ�ǵ�20713��8��С�����Ⲧ��һ�����ֲ��ϣ�ǡ����ˮ��绰����ĸ���Ϊ .
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2013-2014ѧ���п���ѧ�½ڸ�ϰ����������Ǻ�����ϰ���������棩 ���ͣ�ѡ����
��Rt��ABC��,2sin(��+20��)=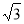 ������Ǧ��Ķ�����
������Ǧ��Ķ�����
A.60�� B.80�� C.40�� D.���Ͻ��۶�����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2013-2014ѧ���п���ѧ�½ڸ�ϰ���Է�����������ϰ���������棩 ���ͣ�ѡ����
y=ax+b��y=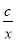 ��ͼ��,��ͼ��ʾ,��
��ͼ��,��ͼ��ʾ,��
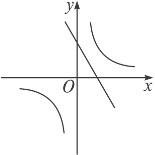
A.a>0,b>0,c>0 B.a<0,b<0,c<0
C.a<0,b>0,c>0 D.a<0,b<0,c>0
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com