
����Ŀ����ͼ1����������ABCD�У���E��F�ֱ��DZ�BC��AB�ϵĵ㣬��CE=BF������DE������E��EG��DE��ʹEG=DE������FG��FC��
��1�����жϣ�FG��CE��������ϵ�� ��λ�ù�ϵ�� ��
��2����ͼ2������E��F�ֱ��DZ�CB��BA�ӳ����ϵĵ㣬�����������䣬��1���н����Ƿ���Ȼ�������������жϲ�����֤����
��3����ͼ3������E��F�ֱ��DZ�BC��AB�ӳ����ϵĵ㣬�����������䣬��1���н����Ƿ���Ȼ��������ֱ��д������ж���
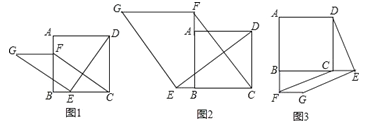
���𰸡���1��FG=CE��FG��CE����2����������3��������
��������
�����������1��ֻҪ֤���ı���CDGF��ƽ���ı��μ��ɵó�FG=CE��FG��CE��
��2�����츨���ߺ�֤����HGE�ա�CED�����ö�Ӧ�������֤�ı���GHBF�Ǿ��κ����õ��������������FG=C��FG��CE��
��3��֤����CBF�ա�DCE����֤���ı���CEGF��ƽ���ı��Σ�
�����������1��FG=CE��FG��CE��
��2������G��GH��CB���ӳ����ڵ�H����EG��DE�����GEH+��DEC=90�㣬�ߡ�GEH+��HGE=90�㣬���DEC=��HGE���ڡ�HGE���CED�У��ߡ�GHE=��DCE����HGE=��DEC��EG=DE�����HGE�ա�CED��AAS������GH=CE��HE=CD����CE=BF����GH=BF����GH��BF�����ı���GHBF�Ǿ��Σ���GF=BH��FG��CH����FG��CE�����ı���ABCD�������Σ���CD=BC����HE=BC����HE+EB=BC+EB����BH=EC����FG=EC��
��3�����ı���ABCD�������Σ���BC=CD����FBC=��ECD=90�㣬�ڡ�CBF���DCE�У���BF=CE����FBC=��ECD��BC=DC�����CBF�ա�DCE��SAS�������BCF=��CDE��CF=DE����EG=DE����CF=EG����DE��EG�����DEC+��CEG=90�����ߡ�CDE+��DEC=90�������CDE=��CEG�����BCF=��CEG����CF��EG�����ı���CEGFƽ���ı��Σ���FG��CE��FG=CE��




| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��װ������һ�ּп˺�T�����п�ÿ������100Ԫ��T��ÿ������60Ԫ�������ڿ�չ������ڼ䣬��ͻ��ṩ�����Żݷ�����
�� ��һ���п���һ��T����
�� �п˺�T���������۵�80%���
��ij�ͻ�Ҫ���÷�װ������п�30����T��x����x >30����
��1�����ÿͻ��������ٹ��п��踶��______Ԫ��T���踶��______Ԫ���ú�x��ʽ�ӱ�ʾ����
���ÿͻ��������ڹ��п��踶��______Ԫ��T���踶��______Ԫ���ú�x��ʽ�ӱ�ʾ����
��2����x=40��ͨ������˵���������١����������ַ��������Ϊ���㣿
��3���������Żݷ�����ͬʱʹ�ã���x=40ʱ�����ܸ���һ�ָ�ΪʡǮ�Ĺ�������д����Ĺ�������˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����9x2+kx+25��һ����ȫƽ��ʽ����ôk��ֵ�ǣ� ��
A.15
B.��5
C.30
D.��30
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪13 = 1 =![]() ��12��22, 13+23=9=
��12��22, 13+23=9=![]() ��22��32,13 + 23 + 33 = 36 =
��22��32,13 + 23 + 33 = 36 =![]() ��32��42, �������������������������⣺
��32��42, �������������������������⣺
(1)13+23+33+43+53=________=![]() �� ( )2 �� ( )2
�� ( )2 �� ( )2
(2)���룺13+23+33+��+n3=___________
(3)����(2)�еĽ��ۼ��㣺��д��������̣�
113+123 + 313+143 + 153+163 + ����+393+403.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ƽ��ֱ������ϵ�У���ABC��������������ֱ�ΪA��0��4����B��3��4����C��4����1����
��1������ƽ��ֱ������ϵ�У�������ABC��
��2������A1B1C1���ABC����x��Գƣ�д��A1��B1��C1�����ꣻ
��3����x�����ҵ�һ��P��ʹ��P����A��B����ľ������С��
��4�����ABC�������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ھ���ABCD�У���F�ڱ�BC�ϣ���AF=AD������D��DE��AF������Ϊ��E
��1����֤��DE=AB��
��2����AΪԲ�ģ�AB��Ϊ�뾶��Բ����AF�ڵ�G����BF=FC=1��������ABG�����������������У�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����һ������ʽ����������֪A=![]() �� B=
�� B= ![]() �� C=
�� C=![]() ��
��
����A ��B ��C ��ֵ������ͬѧ����֮��������ֵ��x���������������������ȷ������˵��������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ABCD�ĶԽ���AC��BD���ڵ�O��EF����O����BC��AD�ֱ��ڵ�E��F���Բ����߶�AE��CF�Ĺ�ϵ����˵��������
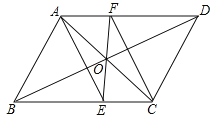
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com