
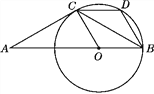
【题目】如图,△ABC是等腰三角形,且AC=BC,∠ACB=120°,在AB上取一点O,使OB=OC,以点O为圆心,OB为半径作圆,过点C作CD∥AB交⊙O于点D,连接BD.
(1)猜想AC与⊙O的位置关系,并证明你的猜想;
(2)试判断四边形BOCD的形状,并证明你的判断;
(3)已知AC=6,求扇形OBC所围成的圆锥的底面圆的半径r.
【答案】(1)猜想:AC与⊙O相切(2)四边形BOCD为菱形(3)![]()
【解析】试题分析:本题考查了切线的判定定理:经过半径的外端且垂直于这条半径的直线是圆的切线.也考查了菱形的判定方法和圆锥的计算.(1)根据等腰三角形的性质得∠A=∠ABC=30°,再由OB=OC得∠OCB=∠OBC=30°,所以∠ACO=∠ACB-∠OCB=90°,然后根据切线的判定定理即可得到,AC是⊙O的切线;
(2)连结OD,由CD∥AB得到∠AOC=∠OCD,根据三角形外角性质得∠AOC=∠OBC+∠OCB=60°,所以∠OCD=60°,于是可判断△OCD为等边三角形,则CD=OB=OC,先可判断四边形OBDC为平行四边形,加上OB=OC,于是可判断四边形BOCD为菱形;(3)在Rt△AOC中,根据含30度的直角三角形三边的关系得到
OC=![]() ∴弧BC的弧长=
∴弧BC的弧长=![]() 然后根据圆锥的计算求圆锥的底面圆半径.
然后根据圆锥的计算求圆锥的底面圆半径.
试题解析(1)AC与⊙O相切
![]() ,∠ACB=120°,∴∠ABC=∠A=30°。
,∠ACB=120°,∴∠ABC=∠A=30°。
![]() ,∠CBO=∠BCO=30°,
,∠CBO=∠BCO=30°,
∴∠OCA=120°-30°=90°,∴AC⊥OC,
又∵OC是⊙O的半径,
∴AC与⊙O相切。
(2)四边形BOCD是菱形
连接OD。
∵CD∥AB,
∴∠OCD=∠AOC=2×30°=60°
![]() ,
,
∴△COD是等边三角形,
![]() ,
,
∴四边形BOCD是平行四边形,
![]()
∴四边形BOCD是菱形。
(3)在Rt△AOC中,∠A=30°,AC=6,
![]() ACtan∠A=6tan30°=
ACtan∠A=6tan30°=![]() ,
,
∴弧BC的弧长![]()
∴底面圆半径![]()


科目:初中数学 来源: 题型:
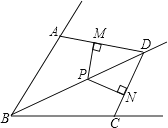
【题目】已知,如图,BD是∠ABC的平分线,AB=BC,点P在BD上,PM⊥AD,PN⊥CD,垂足分别是M、N.
(1)求证:PM=PN;
(2)联结MN,求证:PD是MN的垂直平分线.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,O为矩形ABCD对角线的交点,DE∥AC,CE∥BD.

(1)试判断四边形OCED的形状,并说明理由;
(2)若AB=6,BC=8,求四边形OCED的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
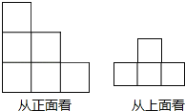
【题目】用小立方块搭成的几何体.从正面看和从上面看的形状如图所示,问组成这样的几何体最多需要多少个立方块,最少需要多少个立方块?请画出最少和最多时从左面看到的形状.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我市某校为了创建书香校园,去年购进一批图书.经了解,科普书的单价比文学书的单价多4元,用12000元购进的科普书与用8000元购进的文学书本数相等.
(1)文学书和科普书的单价各多少钱?
(2)今年文学书和科普书的单价和去年相比保持不变,该校打算用10000元再购进一批文学书和科普书,问购进文学书550本后至多还能购进多少本科普书?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,Rt△ABC的三个顶点分别是A(-3,2),B(0,4),C(0,2).
(1)将△ABC以点C为旋转中心旋转180°,画出旋转后对应的△A1B1C;平移△ABC,若点A的对应点A2的坐标为(0,-4),画出平移后对应的△A2B2C2;
(2)若将△A1B1C绕某一点旋转可以得到△A2B2C2,请直接写出旋转中心的坐标;
(3)在x轴上有一点P,使得PA+PB的值最小,请直接写出点P的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知数轴上两点A、B对应的数分别为﹣1、3,点P为数轴上一动点,其对应的数为x.
(1)若点P到点A、点B的距离相等,求点P对应的数;
(2)数轴上是否存在点P,使点P到点A、点B的距离之和为8?若存在,请求出x的值;若不存在,说明理由;
(3)现在点A、点B分别以2个单位长度/秒和0.5个单位长度/秒的速度同时向右运动,点P以6个单位长度/秒的速度同时从O点向左运动.当点A与点B之间的距离为3个单位长度时,求点P所对应的数是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
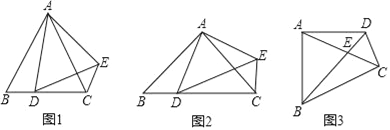
【题目】(1)问题发现
如图1,△ABC和△ADE均为等边三角形,点D在边BC上,连接CE.请填空:
①∠ACE的度数为 ;
②线段AC、CD、CE之间的数量关系为 .
(2)拓展探究
如图2,△ABC和△ADE均为等腰直角三角形,∠BAC=∠DAE=90°,点D在边BC上,连接CE.请判断∠ACE的度数及线段AC、CD、CE之间的数量关系,并说明理由.
(3)解决问题
如图3,在四边形ABCD中,∠BAD=∠BCD=90°,AB=AD=2,CD=1,AC与BD交于点E,请直接写出线段AC的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,AD⊥BC于点D,BE平分∠ABC,若∠ABC=64°,∠AEB=70°.
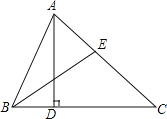
(1)求∠CAD的度数;
(2)若点F为线段BC上的任意一点,当△EFC为直角三角形时,求∠BEF的度数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com