某中学为了让学生的跳远在中考体育测试中取得满意的成绩，在锻炼一个月后，学校对九年级一班的45名学生进行测试，成绩如下表：
| 跳远成绩（cm） | 160 | 170 | 180 | 190 | 200 | 220 |
| 人数 | 3 | 9 | 6 | 9 | 15 | 3 |
这些运动员跳远成绩的中位数和众数分别是
A． 190,200 B．9,9 C．15,9 D．185,200
科目：初中数学 来源： 题型：
如图，AB、AC分别与⊙O相切，切点分别为B、C，过点C作CD∥AB，交⊙O于点D，连接BC、BD．
（1）判断BC与BD的数量关系，并说明理由；
（2）若AB＝9，BC＝6，求⊙O的半径．
查看答案和解析>>
科目：初中数学 来源： 题型：
类比、转化、分类讨论等思想方法和数学基本图形在数学学习和解题中经常用到，如下是一个案例，请补充完整。
原题：如图1，在⊙O中，MN是直径，AB⊥MN于点B，CD⊥MN于点D，∠AOC=90°，AB=3，CD=4，则BD= 。
⑴尝试探究：如图2，在⊙O中，MN是直径，AB⊥MN于点B，CD⊥MN于点D，点E在MN上，∠AEC=90°，AB=3，BD=8，BE：DE=1:3，则CD= （试写出解答过程）。
⑵类比延伸：利用图3，再探究，当A、C两点分别在直径MN两侧，且AB≠CD，AB⊥MN于点B，CD⊥MN于点D，∠AOC=90°时，则线段AB、CD、BD满足的数量关系为 。
⑶拓展迁移：如图4，在平面直角坐标系中，抛物线经过A（m，6），B（n，1）两点（其中0＜m＜3），且以y轴为对称轴，且∠AOB=90°，①求mn的值；②当S△AOB=10时，求抛物线的解析式。
查看答案和解析>>
科目：初中数学 来源： 题型：
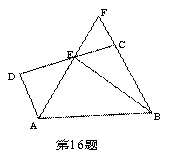
如图。在四边形纸片ABCD中，∠A=130°，∠C=40°，现将其右下角向内折出⊿FGE，折痕为EF，恰使GF∥AD，GE∥CD，则∠B的度数为（ ）
A．90° B．95° C．100° D．105°
查看答案和解析>>
科目：初中数学 来源： 题型：
如图，在梯形ABCD中，AD∥BC，∠D=90°，BC=CD=12，点E在DC上，∠ABE=45°，AE，BC的延长线相交于点F，若AE=10，则S⊿ADE+S⊿CEF的值是 。
查看答案和解析>>
科目：初中数学 来源： 题型：
对于实数定义一种运算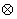
为：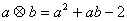
，有下列命题：
①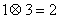
；
②方程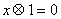
的根为：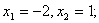
③不等式组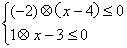
的解集为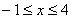
④在函数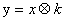
的图像与坐标轴交点组成的三角形面积为3，则此函数的顶点坐标是
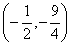其中正确的（ ）
A．①②③④ B．①②③ C．①② D．①②④
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
，恰好有三个整数解，则关于x的一次函数
的图像与反比例函数
的图像的公共点的个数为 。