
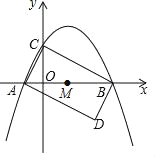
【题目】如图,抛物线y=ax2+bx+2与x轴相交于A(﹣1,0),B(4,0)两点,与y轴相交于点C.
(1)求抛物线的解析式;
(2)将△ABC绕AB中点M旋转180°,得到△BAD.
①求点D的坐标;
②判断四边形ADBC的形状,并说明理由;
(3)在该抛物线对称轴上是否存在点P,使△BMP与△BAD相似?若存在,请求出所有满足条件的P点的坐标;若不存在,请说明理由.
【答案】(1)y=﹣![]() x2+
x2+![]() x+2;(2)①点D的坐标为(3,﹣2),②四边形ADBC为矩形,理由见解析;(3)在该抛物线对称轴上存在点P,使△BMP与△BAD相似,点P的坐标为(
x+2;(2)①点D的坐标为(3,﹣2),②四边形ADBC为矩形,理由见解析;(3)在该抛物线对称轴上存在点P,使△BMP与△BAD相似,点P的坐标为(![]() ,
,![]() )或(
)或(![]() ,﹣
,﹣![]() )或(
)或(![]() ,5)或(
,5)或(![]() ,﹣5).
,﹣5).
【解析】
(1)由点A、B的坐标,利用待定系数法即可求出抛物线的解析式;
(2)利用二次函数图象上点的坐标特征可求出点C的坐标.①过点D作DE⊥x轴于点E,根据旋转的性质可得出OA=EB、OC=ED,结合点A、B、O、C的坐标,即可找出点D的坐标;②由点A、B、C的坐标可得出OA、OC、OB的长度,利用勾股定理可求出AC、BC的长,由AC2+BC2=25=AB2可得出∠ACB=90°,再利用旋转的性质即可找出四边形ADBC为矩形;
(3)假设存在,设点P的坐标为(![]() ,m),由点M为AB的中点可得出∠BPD=∠ADB=90°,分△PMB∽△BDA及△BMP∽△BDA两种情况考虑,利用相似三角形的性质可得出关于m的含绝对值的一元一次方程,解之即可得出结论.
,m),由点M为AB的中点可得出∠BPD=∠ADB=90°,分△PMB∽△BDA及△BMP∽△BDA两种情况考虑,利用相似三角形的性质可得出关于m的含绝对值的一元一次方程,解之即可得出结论.
(1)将A(﹣1,0)、B(4,0)代入y=ax2+bx+2,得:![]() ,解得:
,解得:![]() ,
,
∴抛物线的解析式为y=﹣![]() x2+
x2+![]() x+2.
x+2.
(2)当x=0时,y=﹣![]() x2+
x2+![]() x+2=2,
x+2=2,
∴点C的坐标为(0,2).
①过点D作DE⊥x轴于点E,如图1所示.
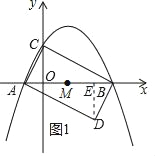
∵将△ABC绕AB中点M旋转180°,得到△BAD,
∴OA=EB,OC=ED.
∵A(﹣1,0),O(0,0),C(0,2),B(4,0),
∴BE=1,DE=2,OE=3,
∴点D的坐标为(3,﹣2).
②四边形ADBC为矩形,理由如下:
∵A(﹣1,0),B(4,0),C(0,2),
∴OA=1,OC=2,OB=4,AB=5,
∴AC=![]() ,BC=
,BC=![]() .
.
∵AC2+BC2=25=AB2,
∴∠ACB=90°.
∵将△ABC绕AB中点M旋转180°,得到△BAD,
∴∠ABC=∠BAD,BC=AD,
∴BC∥AD且BC=AD,
∴四边形ADBC为平行四边形.
又∵∠ACB=90°,
∴四边形ADBC为矩形.
(3)假设存在,设点P的坐标为(![]() ,m).
,m).
∵点M为AB的中点,
∴∠BPD=∠ADB=90°,
∴有两种情况(如图2所示).
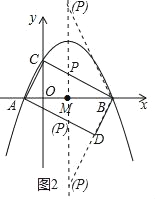
①当△PMB∽△BDA时,有![]() ,即
,即![]() ,
,
解得:m=±![]() ,
,
∴点P的坐标为(![]() ,
,![]() )或(
)或(![]() ,﹣
,﹣![]() );
);
②当△BMP∽△BDA时,有![]() ,即
,即![]() ,
,
解得:m=±5,
∴点P的坐标为(![]() ,5)或(
,5)或(![]() ,﹣5).
,﹣5).
综上所述:在该抛物线对称轴上存在点P,使△BMP与△BAD相似,点P的坐标为(![]() ,
,![]() )或(
)或(![]() ,﹣
,﹣![]() )或(
)或(![]() ,5)或(
,5)或(![]() ,﹣5).
,﹣5).


科目:初中数学 来源: 题型:
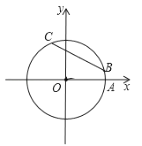
【题目】如图,在平面直角坐标系xOy中,以原点O为圆心的圆过点A(![]() ,0),直线y=kx-2k+3与⊙O交于B、C两点,则弦BC的长的最小值为_______.
,0),直线y=kx-2k+3与⊙O交于B、C两点,则弦BC的长的最小值为_______.
查看答案和解析>>
科目:初中数学 来源: 题型:
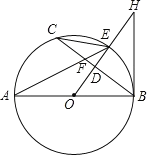
【题目】如图,AB为⊙O的直径,OD⊥弦BC于点D,交⊙O于点E,AE与BC交于点F,点H为OD延长线上一点,且∠OHB=∠AEC.
(1)求证:BH是⊙O的切线;
(2)求证:CE2=EF·EA;
(3)若⊙O的半径为5,sin∠C=![]() ,求BF的长.
,求BF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
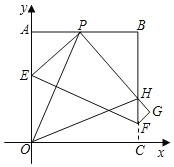
【题目】如图,将一张边长为8的正方形纸片OABC放在直角坐标系中,使得OA与y轴重合,OC与x轴重合,点P为正方形AB边上的一点(不与点A、点B重合).将正方形纸片折叠,使点O落在P处,点C落在G处,PG交BC于H,折痕为EF.连接OP、OH.
初步探究
(1)当AP=4时
①直接写出点E的坐标 ;
②求直线EF的函数表达式.
深入探究
(2)当点P在边AB上移动时,∠APO与∠OPH的度数总是相等,请说明理由.
拓展应用
(3)当点P在边AB上移动时,△PBH的周长是否发生变化?并证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平行四边形ABCD中,点G在边DC的延长线上,AG交边BC于点E,交对角线BD于点F.
(1)求证:AF2=EFFG;
(2)如果EF=![]() ,FG=
,FG=![]() ,求
,求![]() 的值.
的值.
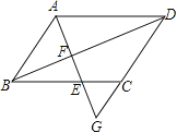
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(阅读材科)小明同学发现这样一个规律:两个顶角相等的等腰三角形,
如果具有公共的项角的顶点,并把它们的底角顶点连接起来则形成一组全等的三角形,小明把具有这个规律的图形称为“手拉手”图形.如图1,在“手拉手”图形中,小明发现若∠BAC=∠DAE,AB=AC,AD=AE,则△ABD≌△ACE.
(材料理解)(1)在图1中证明小明的发现.
(深入探究)(2)如图2,△ABC和△AED是等边三角形,连接BD,EC交于点O,连接AO,下列结论:①BD=EC;②∠BOC=60°;③∠AOE=60°;④EO=CO,其中正确的有 .(将所有正确的序号填在横线上).
(延伸应用)(3)如图3,AB=BC,∠ABC=∠BDC=60°,试探究∠A与∠C的数量关系.
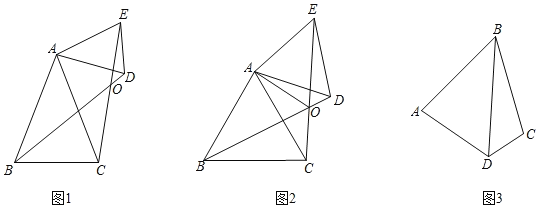
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,![]() 为等腰三角形,
为等腰三角形,![]() ,点
,点![]() 在线段
在线段![]() 上(不与
上(不与![]() 重合),以
重合),以![]() 为腰长作等腰直角
为腰长作等腰直角![]() ,
,![]() 于
于![]() .
.
(1)求证:![]() ;
;
(2)连接![]() 交
交![]() 于
于![]() ,若
,若![]() ,求
,求![]() 的值.
的值.
(3)如图2,过![]() 作
作![]() 于
于![]() 的延长线于点
的延长线于点![]() ,过
,过![]() 点作
点作![]() 交
交![]() 于
于![]() ,连接
,连接![]() ,当点
,当点![]() 在线段
在线段![]() 上运动时(不与
上运动时(不与![]() 重合),式子
重合),式子![]() 的值会变化吗?若不变,求出该值;若变化,请说明理由..
的值会变化吗?若不变,求出该值;若变化,请说明理由..
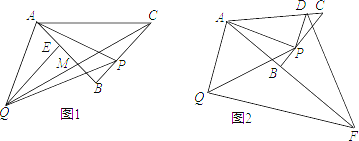
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】![]() 朗读者
朗读者![]() 自开播以来,以其厚重的文化底蕴和感人的人文情怀,感动了数以亿计的观众,岳池县某中学开展“朗读”比赛活动,九年级
自开播以来,以其厚重的文化底蕴和感人的人文情怀,感动了数以亿计的观众,岳池县某中学开展“朗读”比赛活动,九年级![]() 、
、![]() 班根据初赛成绩,各选出5名选手参加复赛,两个班各选出的5名选手的复赛成绩
班根据初赛成绩,各选出5名选手参加复赛,两个班各选出的5名选手的复赛成绩![]() 满分为100分
满分为100分![]() 如图所示.
如图所示.
平均数 | 中位数 | 众数 | |
九 | 85 | 85 | |
九 | 80 |
![]() 根据图示填写表格;
根据图示填写表格;
![]() 结合两班复赛成绩的平均数和中位数,分析哪个班级的复赛成绩较好;
结合两班复赛成绩的平均数和中位数,分析哪个班级的复赛成绩较好;
![]() 如果规定成绩较稳定班级胜出,你认为哪个班级能胜出?说明理由.
如果规定成绩较稳定班级胜出,你认为哪个班级能胜出?说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com