
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
分析 ①根据正多边形的定义进行判断;②根据圆心角、弧、弦的关系进行分析即可;③根据等式的基本性质进行判断;④根据一次函数的性质进行判断即可.
解答 解:①各边相等,各内角相等的多边形是正多边形,原命题是假命题,逆命题是真命题;
②在同圆或等圆中,相等的圆心角所对的弧相等,原命题是假命题,逆命题也是假命题;
③若a2=b2,则a=±b;原命题是假命题,逆命题是真命题;
④直线y=kx+b经过第一、二、四象限,则k<0,b>0,原命题与逆命题都是真命题,
原命题与逆命题都是真命题的个数为1,
故选A.
点评 本题主要考查命题的真假判断,正确的命题叫真命题,错误的命题叫做假命题,判断命题的真假关键是要熟悉课本中的性质定理,需要注意逆命题的写法.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
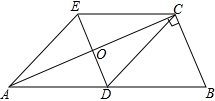 如图,在Rt△ABC中,∠BCA=90°,CD是AB边上的中线,分别过点C,D作BA和BC的平行线,两线交于点E,且DE交AC于点O,连接AE.
如图,在Rt△ABC中,∠BCA=90°,CD是AB边上的中线,分别过点C,D作BA和BC的平行线,两线交于点E,且DE交AC于点O,连接AE.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | (3,-2) | B. | (1,-6) | C. | (-1,6) | D. | (-1,-6) |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 3,2 | B. | 3,4 | C. | 5,2 | D. | 5,4 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com