

分析 (1)有两张完全重合的矩形纸片,小亮同学将其中一张绕点A顺时针旋转90°后得到矩形AMEF(如图1),得BD=MF,△BAD≌△MAF,推出BD=MF,∠ADB=∠AFM=30°,进而可得∠DNM的大小.
(2)分两种情形讨论①当AK=FK时,②当AF=FK时,根据旋转的性质得出结论.
(3)求平移的距离是A2A的长度.在矩形PNA2A中,A2A=PN,只要求出PN的长度就行.用△DPN∽△DAB得出:$\frac{PN}{AB}$=$\frac{DP}{DA}$,解得A2A的大小.
解答 解:(1)结论:BD=MF,BD⊥MF.
理由:如图1中,延长FM交BD于点N,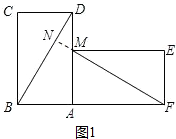
由题意得:△BAD≌△MAF.
∴BD=MF,∠ADB=∠AFM.
又∵∠DMN=∠AMF,
∴∠ADB+∠DMN=∠AFM+∠AMF=90°,
∴∠DNM=90°,
∴BD⊥MF.
(2)如图2中,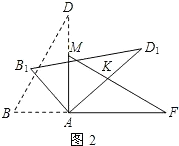
①当AK=FK时,∠KAF=∠F=30°,
则∠BAB1=180°-∠B1AD1-∠KAF=180°-90°-30°=60°,
即β=60°;
②当AF=FK时,∠FAK=$\frac{180°-∠F}{2}$=75°,
∴∠BAB1=90°-∠FAK=15°,
即β=15°;
∴β的度数为60°或15°
(3)如图3中,
由题意得矩形PNA2A.设A2A=x,则PN=x,
在Rt△A2M2F2中,∵F2M2=FM=8,
∴A2M2=4,A2F2=4 $\sqrt{3}$,
∴AF2=4 $\sqrt{3}$-x.
∵∠PAF2=90°,∠PF2A=30°,
∴AP=AF2•tan30°=4-$\frac{\sqrt{3}}{3}$x.
∴PD=AD-AP=4 $\sqrt{3}$-4+$\frac{\sqrt{3}}{3}$x.
∵NP∥AB,
∴∠DNP=∠B.
∵∠D=∠D,∴△DPN∽△DAB.
∴$\frac{PN}{AB}$=$\frac{DP}{DA}$,
∴$\frac{x}{4}$=$\frac{4\sqrt{3}-4+\frac{\sqrt{3}}{3}x}{4\sqrt{3}}$,解得x=6-2 $\sqrt{3}$.
即A2A=6-2 $\sqrt{3}$.
答:平移的距离是(6-2 $\sqrt{3}$)cm.
点评 本题是一道综合性比较强的几何综合试题.考查了旋转的性质,相似三角形的判定与性质,勾股定理的运用,等腰三角形的性质的运用.在利用相似三角形的性质时注意使用相等线段的代换,属于中考压轴题.


 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案科目:初中数学 来源:2016-2017学年江苏省东台市第六教育联盟七年级下学期第一次月考数学试卷 题型:单选题
下面有3句话:①同旁内角互补;②两直线平行,内错角相等;③在同一平面内,垂直于同一条直线的两直线互相平行.其中正确的为 ( )
A. ① B. ② C. ③ D. ②③
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:选择题
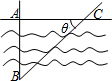 如图,为了测量河两岸A、B两点的距离,在与AB垂直的方向点C处测得AC=a,∠ACB=θ,那么AB等于( )
如图,为了测量河两岸A、B两点的距离,在与AB垂直的方向点C处测得AC=a,∠ACB=θ,那么AB等于( )| A. | a•sinθ | B. | a•tanθ | C. | a•cosθ | D. | $\frac{a}{tanθ}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
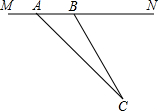 “为了安全,请勿超速”,如图所示是一条已经建成并通车的公路,且该公路的某直线路段MN上限速17m/s,为了检测来往车辆是否超速,交警在MN旁设立了观测点C.若某次从观测点C测得一汽车从点A到达点B行驶了5秒钟,已知∠CAN=45°,∠CBN=60°,BC=200m.
“为了安全,请勿超速”,如图所示是一条已经建成并通车的公路,且该公路的某直线路段MN上限速17m/s,为了检测来往车辆是否超速,交警在MN旁设立了观测点C.若某次从观测点C测得一汽车从点A到达点B行驶了5秒钟,已知∠CAN=45°,∠CBN=60°,BC=200m.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
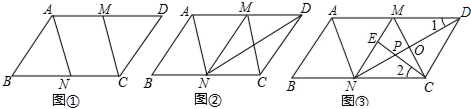
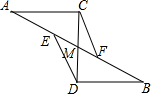 如图,AC=BD,∠A=∠B,点E、F在AB上,且DE∥CF,CD与AB交于点M,小明经过研究发现该图形是中心对称图形,则该图形的对称中心是点M.
如图,AC=BD,∠A=∠B,点E、F在AB上,且DE∥CF,CD与AB交于点M,小明经过研究发现该图形是中心对称图形,则该图形的对称中心是点M.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com