





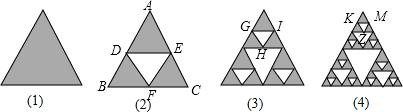
 BC,推出△ADE∽△ABC,
BC,推出△ADE∽△ABC, =
= ,求出△DEF∽△ACB,推出△DEF和△ACB的面积比是(
,求出△DEF∽△ACB,推出△DEF和△ACB的面积比是( )2=
)2= ,求出△DEF的面积,同理求出△GHI和△KZM的面积,根据图形求出即可.
,求出△DEF的面积,同理求出△GHI和△KZM的面积,根据图形求出即可. BC,
BC, =
= ,
, =(
=( )2=
)2= ,
,
 BC,EF=
BC,EF= AB,DF=
AB,DF= AC,
AC, =
= =
=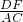 =
= ,
,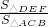 =(
=( )2=
)2= ,
, ,
, S△ABC=
S△ABC= ,
, =
= ,
, ×
× =
= ,
,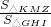 =
= ,
, ×
× =
=
 -3×
-3× -9×
-9× =
= .
.

 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
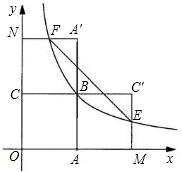 如图,四边形OABC是面积为4的正方形,函数y=
如图,四边形OABC是面积为4的正方形,函数y=| k |
| x |
| k |
| x |
查看答案和解析>>
科目:初中数学 来源: 题型:
 (2013•本溪)如图,点B1是面积为1的等边△OBA的两条中线的交点,以OB1为一边,构造等边△OB1A1(点O,B1,A1按逆时针方向排列),称为第一次构造;点B2是△OB1A1的两条中线的交点,再以OB2为一边,构造等边△OB2A2(点O,B2,A2按逆时针方向排列),称为第二次构造;以此类推,当第n次构造出的等边△OBnAn的边OAn与等边△OBA的边OB第一次重合时,构造停止.则构造出的最后一个三角形的面积是
(2013•本溪)如图,点B1是面积为1的等边△OBA的两条中线的交点,以OB1为一边,构造等边△OB1A1(点O,B1,A1按逆时针方向排列),称为第一次构造;点B2是△OB1A1的两条中线的交点,再以OB2为一边,构造等边△OB2A2(点O,B2,A2按逆时针方向排列),称为第二次构造;以此类推,当第n次构造出的等边△OBnAn的边OAn与等边△OBA的边OB第一次重合时,构造停止.则构造出的最后一个三角形的面积是| 1 |
| 310 |
| 1 |
| 310 |
查看答案和解析>>
科目:初中数学 来源: 题型:
 (2012•吴中区一模)如图,四边形OABC是面积为4的正方形,函数y=
(2012•吴中区一模)如图,四边形OABC是面积为4的正方形,函数y=| k |
| x |
| k |
| x |
查看答案和解析>>
科目:初中数学 来源: 题型:
 (2011•路南区一模)如图,四边形OABC是面积为4的正方形,函数y=
(2011•路南区一模)如图,四边形OABC是面积为4的正方形,函数y=| k |
| x |
| k |
| x |
| k |
| x |
查看答案和解析>>
科目:初中数学 来源: 题型:

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com