解答:解:(1)∵AB边的垂直平分线交直线BC于点D,垂足为点F,AC边的垂直平分线交直线BC于点E,垂足为点G,
∴∠B=∠BAD,∠C=∠CAE①,
∵∠B+∠BAD+∠C+∠CAE+∠DAE=180°②,∠BAD+∠CAE+∠DAE=100°③,
①②③联立得∠DAE=20°;(2分)
(2)∠DAE=2|90°-∠BAC|(4分)
或∠DAE=2∠BAC.(5分)
即当∠BAC≥90°时,∠DAE=2(∠BAC-90°);
当∠BAC<90°且∠B及∠C均为锐角时,
∠DAE=2(90°-∠BAC);
当∠BAC<90°且∠B、∠C两者之一为钝角时,
∠DAE=2∠BAC.
证明:(I)①当∠BAC>90°时,如图1,
∵∠B+∠BAC+∠C=180°,
∠B+∠1+∠2+∠3+∠C=180°,
∵DF垂直平分AB,
∴DB=DA,
∴∠B=∠1.同理得∠C=∠3,代入式,得:2∠B+∠2+2∠C=180°,
∠2=180°-2(∠B+∠C)=180°-2(180°-∠BAC)=2(∠BAC-90°),(7分)
即∠DAE=2(∠BAC-90°);

②当∠BAC=90°时,如图2,此时,点D、E重合,即
∠DAE=0°,而∠BAC-90°=0°,
∴∠DAE=2(∠BAC-90°)(8分)
(II)当∠BAC<90°且∠B及∠C均为锐角时,①点D、E均在线段BC上,
如图3,∵∠B+∠BAC+∠C=180°,即∠B+∠1+∠2+∠3+∠C=180°,
∵DF垂直平分AB,∴DB=DA,
∴∠B=∠1+∠2,∴∠1=∠B-∠2,
同理得∠3=∠C-∠2,代入上式,得∠B+(∠B-∠2)+∠2+(∠C-∠2)+∠C=180°,
整理得∠2=2(∠B+∠C-90°)=2(180°-∠BAC-90°)=2(∠BAC-90°),
即∠DAE=2(90°-∠BAC);(10分)
②当点D在线段BC上,点E在线段CB的延长线上(如图4)时,
∵EG垂直平分AC,
∴EC=EA,∠C=∠EAC,即∠C=∠1+∠2+∠3,
两边都加∠2,得∠C+∠2=∠1+∠2+∠3+∠2,而DA=DB,
∴∠2=∠ABC,上式即为∠ABC+∠C=∠DAE+∠BAC,
∴∠DAE=∠ABC+∠C-∠BAC=180°-∠BAC-∠BAC=2(90°-∠BAC),
即∠DAE=2(90°-∠BAC);
③当点E在线段BC上,点D在线段BC的延长线上(如图5)时,
∵DF垂直平分AB,
∴DB=DA,∠B=∠BAD,即∠B=∠1+∠2+∠3,
两边都加∠2,得∠B+∠2=∠1+∠2+∠3+∠2,而EA=EC,
∴∠2=∠ACE,上式即为∠B+∠ACB=∠BAC+∠DAE,
∴∠DAE=∠B+∠ACB-∠BAC=180°-∠BAC-∠BAC=2(90°-∠BAC),
即∠DAE=2(90°-∠BAC);

④当点D、E分别在线段BC的延长线和反向延长线上(如图6)时,∠2+∠ABC+∠ACB=180°,等式两边都加上∠1+∠2+∠3,得
(∠1+∠2+∠3)+∠2+∠ABC+∠ACB=180°+(∠1+∠2+∠3),由∠1+∠2=∠ACB,∠2+∠3=∠ABC,∠1+∠2+∠3=∠DAE,得2(∠ABC+∠ACB)=180°+∠DAE,
整理得∠DAE=2(90°-∠BAC);
⑤当点D与点C重合(如图7)时,∠DAE=∠1+∠2,两边都加上∠2,得∠DAE+∠2=∠1+∠2+∠2,由∠2=∠BAC=∠ABC,∠1+∠2=∠BCA,得∠DAE+∠BAC=∠ACB+∠ABC,∠DAE+∠BAC=180°-∠BAC,得∠DAE=2(90°-∠BAC);
⑥当点E与点B重合(如图8)时,∠DAE=∠1+∠2,两边都加上∠1,得∠DAE+∠1=∠1+∠2+∠1,由∠1=∠BAC=∠ACB,∠1+∠2=∠ABC,得∠DAE+∠BAC=∠ACB+∠ABC,∠DAE+∠BAC=180°-∠BAC,得∠DAE=2(90°-∠BAC);

⑦当点D与C重合,点E与B重合时,如图9,由已知条件得BA=BC,CA=CB,从而△ABC为等边三角形,∠DAE=∠A=60°=2(90°-60°)=2(90°-∠A),即∠DAE=2(90°-∠BAC);(12分)
(III)当∠BAC<90°且∠B或∠C之一为钝角时,①设∠ACB为钝角,如图10,
∵EG垂直平分AC,
∴EA=EC,
∴∠ACE=∠3,
又∵∠ACE=∠B+∠BAC=∠B+∠1+∠2,即∠3=∠B+∠1+∠2,两边都加上∠2,
∠3+∠2=∠B+∠1+∠2+∠2,
∵∠3+∠2=∠DAE,∠1+∠2=∠BAC,∠1=∠B,代入得:∠DAE=∠1+∠1+∠2+∠2=2(∠1+∠2)=2∠BAC,即∠DAE=2∠BAC;②当点D与点C重合(∠ACB为钝角)时,如图11,
∵EA=EC,
∴∠2=∠ACE,
∵∠ACE=∠1+∠B=2∠1,即∠DAE=2∠BAC;
③当∠ABC为钝角时,如图12,
∵∠1=∠ABD,而∠ABD=∠2+∠3+∠C,
∴∠1=∠2+∠3+∠C,两边都加∠2,得
∠1+∠2=∠2+∠3+∠C+∠2,∠DAE=∠BAC+∠BAC=2∠BAC;
④当点E与点B重合(∠ABC为钝角)时,如图13,
∵DA=DB,∴∠1=∠ABD,∵∠ABD=∠2+∠C=2∠2,即∠DAE=2∠BAC;(14分)
综上所述,得∠DAE=2(∠BAC-90°)或∠DAE=2(90°-∠BAC)或∠DAE=2∠BAC,即∠DAE=2|90°-∠BAC|或∠DAE=2∠BAC.


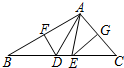 25、在△ABC中,AB边的垂直平分线交直线BC于点D,垂足为点F,AC边的垂直平分线交直线BC于点E,垂足为点G.
25、在△ABC中,AB边的垂直平分线交直线BC于点D,垂足为点F,AC边的垂直平分线交直线BC于点E,垂足为点G.





 17、在△ABC中,AB边的垂直平分线交BC于点D,垂足为点F,AC边的垂直平分线交BC于点E,垂足为点G.
17、在△ABC中,AB边的垂直平分线交BC于点D,垂足为点F,AC边的垂直平分线交BC于点E,垂足为点G. 如图,在△ABC中,AB边的垂直平分线分别交AB、BC于M、P点,AC边的垂直平分线分别交AC、BC于N、Q点.如果∠B=42°,∠C=36°,那么∠PAQ的度数是
如图,在△ABC中,AB边的垂直平分线分别交AB、BC于M、P点,AC边的垂直平分线分别交AC、BC于N、Q点.如果∠B=42°,∠C=36°,那么∠PAQ的度数是 在△ABC中,AB边的垂直平分线交BC于点D,垂足为点F,AC边的垂直平分线交BC于点E,垂足为点G.
在△ABC中,AB边的垂直平分线交BC于点D,垂足为点F,AC边的垂直平分线交BC于点E,垂足为点G.