
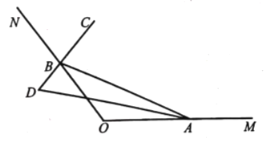
【题目】如图,已知点![]() 分别在
分别在![]() 的边
的边![]() 上运动(不与点
上运动(不与点![]() 重合),
重合),![]() 是
是![]() 的平分线,
的平分线,![]() 的延长线交角
的延长线交角![]() 的平分线于点
的平分线于点![]() .
.
(1)若![]() ,求
,求![]() 的度数.
的度数.
(2)若![]() ,求
,求![]() 的度数.
的度数.
(3)若![]() ,请用含
,请用含![]() 的代数式表示
的代数式表示![]() 的度数.
的度数.
【答案】(1) 144°;(2)60°;(3)![]()
【解析】
(1)根据三角形外角性质可得:∠ABN=∠MON+∠OAB,从而求得∠OAB的度数,再由邻补角的性质可求得![]() 的度数;
的度数;
(2) 根据三角形外角性质可得:∠ABN=∠MON+∠OAB,从而求得∠ABN的度数,再由![]() ∠ABN=∠D+
∠ABN=∠D+![]() 即可求得
即可求得![]() 的度数;
的度数;
(3)方法与(2)方法相同.
(1)∵∠ABN是△AOB的一个外角,
∴∠ABN=∠MON+∠OAB,
又∵![]() ,
,
∴∠OAB=156°-120°=36°,
又∵∠BAM+∠OAB=180°,
∴∠BAM=180°-36°=144°;
(2) ∵∠ABN是△AOB的一个外角,
∴∠ABN=∠MON+∠OAB,
又∵![]() ,
,
∴∠ABN=120°+32°=152°,
又∵![]() 是
是![]() 的平分线,
的平分线,![]() 的延长线交角
的延长线交角![]() 的平分线于点
的平分线于点![]() ,
,
∴![]() ∠ABN=∠D+
∠ABN=∠D+![]() ,
,
∴76°=∠D+16°,
∴∠D=60°;
(3) ∵∠ABN是△AOB的一个外角,
∴∠ABN=∠MON+∠OAB,
又∵![]() 是
是![]() 的平分线,
的平分线,![]() 的延长线交角
的延长线交角![]() 的平分线于点
的平分线于点![]() ,
,
∴![]() ∠ABN=∠D+
∠ABN=∠D+![]() ,
,
∴![]() (∠MON+∠OAB)= ∠D+
(∠MON+∠OAB)= ∠D+![]() ,
,
∴∠D=![]() ∠MON;
∠MON;
又∵![]() ,
,
∴∠D=![]() no.
no.


科目:初中数学 来源: 题型:
【题目】一辆客车从甲地开往乙地,一辆出租车从乙地开往甲地,两车同时出发,设客车离甲地的距离为![]() 千米,出租车离甲地的距离为
千米,出租车离甲地的距离为![]() 千米,两车行驶的时间为x小时,
千米,两车行驶的时间为x小时,![]() 、
、![]() 关于x的图象如图所示:
关于x的图象如图所示:

(1)根据图象,分别写出![]() 、
、![]() 关于x的关系式(需要写出自变量取值范围);
关于x的关系式(需要写出自变量取值范围);
(2)当两车相遇时,求x的值;
(3)甲、乙两地间有![]() 、
、![]() 两个加油站,相距200千米,若客车进入
两个加油站,相距200千米,若客车进入![]() 加油站时,出租车恰好进入
加油站时,出租车恰好进入![]() 加油站,求
加油站,求![]() 加油站离甲地的距离.
加油站离甲地的距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在如图所示的正方形网格中,每个小正方形的边长为1,格点三角形(顶点是网格线的交点的三角形)![]() 在如图所示的位置.
在如图所示的位置.
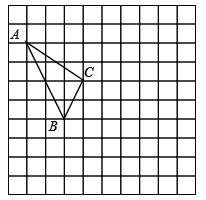
(1)将![]() 向右平移4个单位,向下平移3个单位得△
向右平移4个单位,向下平移3个单位得△![]() ,请在网格中作出△
,请在网格中作出△![]() ;
;
(2)若连接![]() ,
,![]() ,则这两条线段的位置关系是 ;
,则这两条线段的位置关系是 ;
(3)![]() 的面积为 ;
的面积为 ;
(4)在整个平移过程中,![]() 点的运动路径长为 .
点的运动路径长为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】 观察下列等式:
第1个等式:a1=![]() =
=![]() ×(
×(![]() ﹣
﹣![]() );
);
第2个等式:a2=![]() =
=![]() ×(
×(![]() ﹣
﹣![]() );
);
第3个等式:a3=![]() =
=![]() ×(
×(![]() ﹣
﹣![]() );
);
第4个等式:a4=![]() =
=![]() ×(
×(![]() ﹣
﹣![]() );
);
…
请解答下列问题:
(1)按以上规律列出第5个等式:a5= = ;
第n(n为正整数)个等式:an= = ;
(2)求a1+a2+a3+a4+…+a2019的值;
(3)数学符号![]() =f(1)+f(2)+f(3)+…+f(n),试求
=f(1)+f(2)+f(3)+…+f(n),试求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
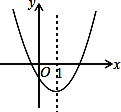
【题目】如图是二次函数y=ax2+bx+c的图象的一部分,对称轴是直线x=1.
①b2>4ac; ②4a-2b+c<0; ③不等式ax2+bx+c>0的解集是x≥3.5; ④若(-2,y1),(5,y2)是抛物线上的两点,则y1<y2.
上述4个判断中,正确的是( )
A. ①② B. ①④ C. ①③④ D. ②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,对于点
中,对于点![]() ,我们把点
,我们把点![]() 叫做点
叫做点![]() 的伴随点。已知点
的伴随点。已知点![]() 的伴随点为
的伴随点为![]() ,点
,点![]() 的伴随点为
的伴随点为![]() ,点
,点![]() 的伴随点为
的伴随点为![]() ,…,这样依次得到点
,…,这样依次得到点![]() 。若点
。若点![]() 的坐标为
的坐标为![]() ,则
,则![]() 的坐标为________。
的坐标为________。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD为平行四边形,∠BAD的角平分线AF交CD于点E,交BC的延长线于点F.
(1)求证:BF=CD;
(2)连接BE,若BE⊥AF,∠BFA=60°,BE=![]() ,求平行四边形ABCD的周长.
,求平行四边形ABCD的周长.

查看答案和解析>>
科目:初中数学 来源: 题型:
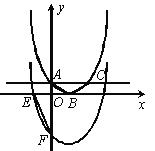
【题目】已知抛物线![]() 与
与![]() 轴只有一个交点,且与
轴只有一个交点,且与![]() 轴交于
轴交于![]() 点,如图,设它的顶点为B.
点,如图,设它的顶点为B.
(1)求![]() 的值;
的值;
(2)过A作x轴的平行线,交抛物线于点C,求证:△ABC是等腰直角三角形;
(3)将此抛物线向下平移4个单位后,得到抛物线![]() ,且与x轴的左半轴交于E点,与y轴交于F点,如图.请在抛物线
,且与x轴的左半轴交于E点,与y轴交于F点,如图.请在抛物线![]() 上求点P,使得△
上求点P,使得△![]() 是以EF为直角边的直角三角形?
是以EF为直角边的直角三角形?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,D、E分别是AB、AC的中点,BE=2DE,延长DE到点F,使得EF=BE,连接CF.
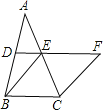
(1)求证:四边形BCFE是菱形;
(2)若CE=4,∠BCF=120°,求菱形BCFE的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com